
【題目】如圖1,在平面直角坐標系中,直線y=x+4與拋物線y=﹣![]() x2+bx+c(b,c是常數)交于A、B兩點,點A在x軸上,點B在y軸上.設拋物線與x軸的另一個交點為點C.
x2+bx+c(b,c是常數)交于A、B兩點,點A在x軸上,點B在y軸上.設拋物線與x軸的另一個交點為點C.

(1)求該拋物線的解析式;
(2)P是拋物線上一動點(不與點A、B重合),
①如圖2,若點P在直線AB上方,連接OP交AB于點D,求![]() 的最大值;
的最大值;
②如圖3,若點P在x軸的上方,連接PC,以PC為邊作正方形CPEF,隨著點P的運動,正方形的大小、位置也隨之改變.當頂點E或F恰好落在y軸上,直接寫出對應的點P的坐標.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②P點坐標(
;②P點坐標(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,2 )(
,2 )(![]() ,2 )
,2 )
【解析】
(1)利用直線解析式求出點A、B的坐標,再利用待定系數法求二次函數解析式即可;
(2)作PF∥BO交AB于點F,證△PFD∽△OBD,得比例線段![]() ,則PF取最大值時,求得
,則PF取最大值時,求得![]() 的最大值;
的最大值;
(3)(i)點F在y軸上時,過點P作PH⊥x軸于H,根據正方形的性質可證明△CPH≌△FCO,根據全等三角形對應邊相等可得PH=CO=2,然后利用二次函數解析式求解即可;(ii)點E在y軸上時,過點PK⊥x軸于K,作PS⊥y軸于S,同理可證得△EPS≌△CPK,可得PS=PK,則P點的橫縱坐標互為相反數,可求出P點坐標;點E在y軸上時,過點PM⊥x軸于M,作PN⊥y軸于N,同理可證得△PEN≌△PCM,可得PN=PM,則P點的橫縱坐標相等,可求出P點坐標.
解:(1)直線y=x+4與坐標軸交于A、B兩點,
當x=0時,y=4,x=﹣4時,y=0,
∴A(﹣4,0),B(0,4),
把A,B兩點的坐標代入解析式得,![]() ,解得,
,解得,![]() ,
,
∴拋物線的解析式為![]() ;
;
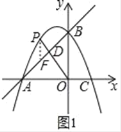
(2)①如圖1,作PF∥BO交AB于點F,
∴△PFD∽△OBD,
∴![]() ,
,
∵OB為定值,
∴當PF取最大值時,![]() 有最大值,
有最大值,
設P(x,![]() ),其中﹣4<x<0,則F(x,x+4),
),其中﹣4<x<0,則F(x,x+4),
∴PF=![]() =
=![]() ,
,
∵![]() 且對稱軸是直線x=﹣2,
且對稱軸是直線x=﹣2,
∴當x=﹣2時,PF有最大值,
此時PF=2,![]()
![]() ;
;
②∵點C(2,0),
∴CO=2,
(i)如圖2,點F在y軸上時,過點P作PH⊥x軸于H,
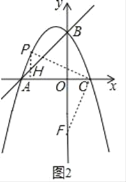
在正方形CPEF中,CP=CF,∠PCF=90°,
∵∠PCH+∠OCF=90°,∠PCH+∠HPC=90°,
∴∠HPC=∠OCF,
在△CPH和△FCO中, ,
,
∴△CPH≌△FCO(AAS),
∴PH=CO=2,
∴點P的縱坐標為2,
∴![]() ,
,
解得,![]() ,
,
∴![]() ,
,![]() ,
,
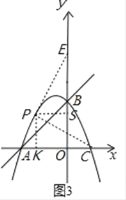
(ii)如圖3,點E在y軸上時,過點PK⊥x軸于K,作PS⊥y軸于S,
同理可證得△EPS≌△CPK,
∴PS=PK,
∴P點的橫縱坐標互為相反數,
∴![]() ,
,
解得x=2![]() (舍去),x=﹣2
(舍去),x=﹣2![]() ,
,
∴![]() ,
,
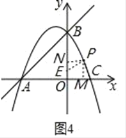
如圖4,點E在y軸上時,過點PM⊥x軸于M,作PN⊥y軸于N,
同理可證得△PEN≌△PCM
∴PN=PM,
∴P點的橫縱坐標相等,
∴![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
∴![]() ,
,
綜合以上可得P點坐標(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,2 )(
,2 )(![]() ,2 ).
,2 ).


科目:初中數學 來源: 題型:
【題目】(1)(問題發現)
如圖1,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,延長CA到點F,使得AF=AC,連接DF、BE,則線段BE與DF的數量關系為 ,位置關系為 ;
(2)(拓展研究)
將△ADE繞點A旋轉,(1)中的結論有無變化?僅就圖(2)的情形給出證明;
(3)(解決問題)
當AB=2,AD=![]() ,△ADE旋轉得到D,E,F三點共線時,直接寫出線段DF的長.
,△ADE旋轉得到D,E,F三點共線時,直接寫出線段DF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某家具生產廠生產某種配套桌椅(一張桌子,兩把椅子),已知每塊板材可制作桌子![]() 張或椅子
張或椅子![]() 把,現計劃用
把,現計劃用![]() 塊這種板材生產一批桌椅(不考慮板材的損耗,恰好配套),設用
塊這種板材生產一批桌椅(不考慮板材的損耗,恰好配套),設用![]() 塊板材做椅子,用
塊板材做椅子,用![]() 塊板材做桌子,則下列方程組正確的是( )
塊板材做桌子,則下列方程組正確的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校計劃為疫情期間表現優秀的學生購買獎品.已知購買![]() 個
個![]() 獎品和
獎品和![]() 個
個![]() 獎品共需
獎品共需![]() 元;購買
元;購買![]() 個
個![]() 獎品和
獎品和![]() 個
個![]() 獎品共需
獎品共需![]() 元
元
(1)求![]() 兩種獎品的單價;
兩種獎品的單價;
(2)學校準備購買![]() 兩種獎品共
兩種獎品共![]() 個,且
個,且![]() 獎品的數量不少于
獎品的數量不少于![]() 獎品數量的一半,請設計出最省錢的購買方案,并說明理由.
獎品數量的一半,請設計出最省錢的購買方案,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
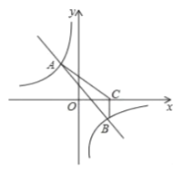
【題目】如圖,一次函數![]() 與反比例函數
與反比例函數![]() 的圖象交于
的圖象交于![]() 兩點.
兩點.
(1)求一次函數與反比例函數的解析式;
(2)根據已知條件,請直接寫出不等式![]() 的解集;
的解集;
(3)過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】五一小長假前夕,某服裝店的老板到服裝廠購買男士夏裝和女士夏裝.已知購進![]() 套男士夏裝和
套男士夏裝和![]() 套女士夏裝需要
套女士夏裝需要![]() 元;購進
元;購進![]() 套男士夏裝和
套男士夏裝和![]() 套女士夏裝需要
套女士夏裝需要![]() 元.
元.
(1)求男士夏裝和女士夏裝每套進價分別是多少元;
(2)若![]() 套男士夏裝的售價為
套男士夏裝的售價為![]() 元,
元,![]() 套女士夏裝的售價為
套女士夏裝的售價為![]() 元,時裝店決定購進男士夏裝的數量為女士夏裝的數量的
元,時裝店決定購進男士夏裝的數量為女士夏裝的數量的![]() 還多
還多![]() 套,如果購進的男士夏裝和女士夏裝全部售出后的總利潤超過
套,如果購進的男士夏裝和女士夏裝全部售出后的總利潤超過![]() 元,那么此次至少可購進多少套女士夏裝?
元,那么此次至少可購進多少套女士夏裝?
查看答案和解析>>
科目:初中數學 來源: 題型:
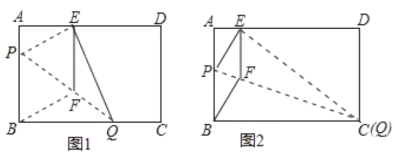
【題目】如圖1,在矩形紙片![]() 中,
中,![]() ,
,![]() ,折疊紙片使
,折疊紙片使![]() 點落在邊
點落在邊![]() 上的
上的![]() 處,折痕為
處,折痕為![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]() .
.
(1)求證:四邊形![]() 為菱形;
為菱形;
(2)當點![]() 在
在![]() 邊上移動時,折痕的端點
邊上移動時,折痕的端點![]() 也隨之移動;
也隨之移動;
①當點![]() 與點
與點![]() 重合時(如圖2),求菱形
重合時(如圖2),求菱形![]() 的邊長;
的邊長;
②若限定![]() 分別在邊
分別在邊![]() 上移動,求出點
上移動,求出點![]() 在邊
在邊![]() 上移動的最大距離.
上移動的最大距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
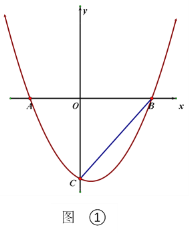
【題目】如圖,拋物線![]() 交x軸于A、B兩點(點A在點B的左側),
交x軸于A、B兩點(點A在點B的左側),![]() .
.
(1)求拋物線的函數表達式;
(2)如圖①,連接BC,點P在拋物線上,且∠BCO=![]() ∠PBA.求點P的坐標
∠PBA.求點P的坐標
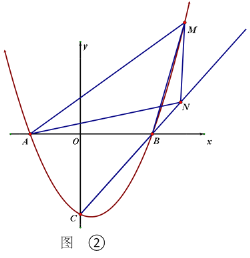
(3)如圖②,M是拋物線上一點,N為射線CB上的一點,且M、N兩點均在第一象限內,B、N是位于直線AM同側的不同兩點,![]() ,點M到
,點M到![]() 軸的距離為2L,△AMN的面積為5L,且∠ANB=∠MBN,請問MN的長是否為定值?如果是,請求出這個定值;如果不是,請說明理由.
軸的距離為2L,△AMN的面積為5L,且∠ANB=∠MBN,請問MN的長是否為定值?如果是,請求出這個定值;如果不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com