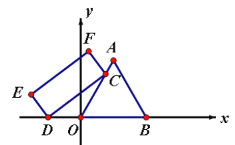
【題目】如圖，等邊△AOB，點C是邊AO所在直線上的動點，點D是x軸上的動點，在矩形CDEF中，CD=6，DE=
，則OF的最小值為___________．
科目：初中數學 來源： 題型：
【題目】某公司投入研發費用40萬元(40萬元只計入第一年成本)，成功研發出一種產品．公司按訂單生產(產量＝銷售量)，第一年該產品正式投產后，生產成本為4元/件．此產品年銷售量y(萬件)與售價x(元件)之間滿足函數關系式y＝﹣x+20．
(1)求這種產品第一年的利潤W(萬元)與售價x(元件)滿足的函數關系式；
(2)該產品第一年的利潤為24萬元，那么該產品第一年的售價是多少？
(3)第二年，該公司將第一年的利潤24萬元(24萬元只計入第二年成本)再次投入研發，使產品的生產成本降為3元/件．為保持市場占有率，公司規定第二年產品售價不超過第一年的售價，另外受產能限制，銷售量無法超過10萬件．請計算該公司第二年的利潤W2至少為多少萬元．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】詩詞是中華民族燦爛文化中的瑰寶，王老師連續三個月在班上開展針對全班同學的古詩詞默寫的測試活動．如圖，王老師將三次默寫的成績（滿分10分）做了統計，并繪制了折線統計圖．由圖可知，以下結論錯誤的是（ ）
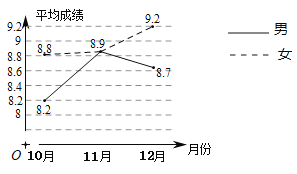
A.男、女生11月份的平均成績相同
B.10月到12月，女生的平均成績一直在進步
C.10月到11月，女生的平均成績的增長率約為8.5%
D.11月到12月女生的平均成績比10月到11月的增長快
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，拋物線y=﹣
x2+bx+c與x軸交于點A(﹣1，0)和點B(3，0)．P為該拋物線上一動點，設點P的橫坐標為m．
（1）求拋物線的解析式．
（2）將該拋物線沿y軸向下平移AB個單位長度，點P的對應點為P′，若OP=OP′，求△OP P′的面積．
（3）如圖2，連接AP，BP，設△APB的面積為S，當-2≤m≤2時，直接寫出S的最大值．
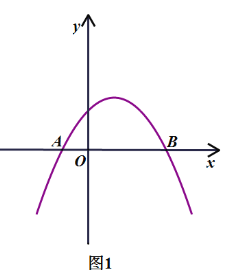
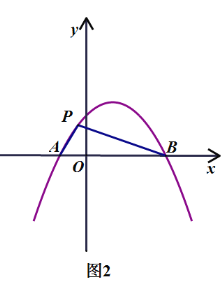
查看答案和解析>>
科目：初中數學 來源： 題型：
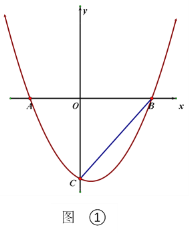
【題目】如圖，拋物線
交x軸于A、B兩點（點A在點B的左側），
．
（1）求拋物線的函數表達式；
（2）如圖①，連接BC，點P在拋物線上，且∠BCO=
∠PBA．求點P的坐標
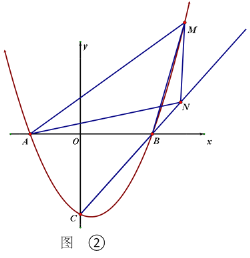
（3）如圖②，M是拋物線上一點，N為射線CB上的一點，且M、N兩點均在第一象限內，B、N是位于直線AM同側的不同兩點，
，點M到
軸的距離為2L，△AMN的面積為5L，且∠ANB=∠MBN，請問MN的長是否為定值？如果是，請求出這個定值；如果不是，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，正方形ABCD的邊長為4，點E，F分別在邊AB，AD上，且∠ECF＝45°，CF的延長線交BA的延長線于點G，CE的延長線交DA的延長線于點H，連接AC，EF．，GH．
（1）填空：∠AHC ∠ACG；（填“＞”或“＜”或“＝”）
（2）線段AC，AG，AH什么關系？請說明理由；
（3）設AE＝m，
①△AGH的面積S有變化嗎？如果變化．請求出S與m的函數關系式；如果不變化，請求出定值．
②請直接寫出使△CGH是等腰三角形的m值．
查看答案和解析>>
科目：初中數學 來源： 題型：
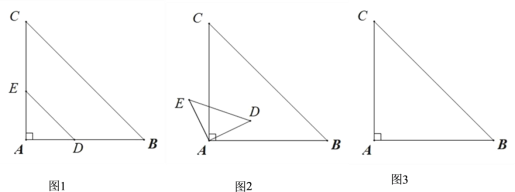
【題目】如圖 1，在等腰直角△ABC 中，∠A =90°，AB=AC=3，在邊 AB 上取一點 D（點 D 不與點 A，B 重合），在邊 AC 上取一點 E，使 AE=AD，連接 DE. 把△ADE 繞點 A 逆時針方向旋轉α（0°＜α＜360°），如圖 2．
（1）請你在圖 2 中，連接 CE 和 BD，判斷線段 CE 和 BD 的數量關系，并說明理由；
（2）請你在圖 3 中，畫出當α =45°時的圖形，連接 CE 和 BE，求出此時△CBE 的面積；
（3）若 AD=1，點 M 是 CD 的中點，在△ADE 繞點 A 逆時針方向旋轉的過程中，線段AM 的最小值是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知矩形OABC的一個頂點B的坐標是（4，2），反比例函數y=
（x＞0）的圖象經過矩形的對稱中點E，且與邊BC交于點D，若過點D的直線y=mx+n將矩形OABC的面積分成3：5的兩部分，則此直線的解析式為_____．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
