
【題目】如圖,在![]() 中,
中,![]() ,
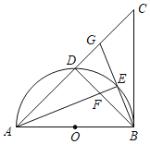
,![]() ,以AB為直徑的半圓O交AC于點D,點E是
,以AB為直徑的半圓O交AC于點D,點E是![]() 上不與點B,D重合的任意一點,連接AE交BD于點F,連接BE并延長交AC于點G.
上不與點B,D重合的任意一點,連接AE交BD于點F,連接BE并延長交AC于點G.
(1)求證:![]() ;
;
(2)填空:
①若![]() ,且點E是
,且點E是![]() 的中點,則DF的長為 ;
的中點,則DF的長為 ;
②取![]() 的中點H,當
的中點H,當![]() 的度數為 時,四邊形OBEH為菱形.
的度數為 時,四邊形OBEH為菱形.
科目:初中數學 來源: 題型:
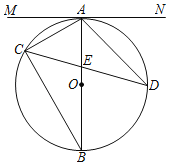
【題目】如圖,△ABC內接于⊙O,AB是⊙O的直徑,弦CD與AB交于點E,連接AD,過點A作直線MN,使∠MAC=∠ADC.
(1)求證:直線MN是⊙O的切線.
(2)若sin∠ADC=![]() ,AB=8,AE=3,求DE的長.
,AB=8,AE=3,求DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】交通工程學理論把在單向道路上行駛的汽車看成連續的流體,并用流量、速度、密度三個概念描述車流的基本特征,其中流量q(輛/小時)指單位時間內通過道路指定斷面的車輛數;速度v(千米/小時)指通過道路指定斷面的車輛速度,密度k(輛/千米)指通過道路指定斷面單位長度內的車輛數.
為配合大數據治堵行動,測得某路段流量q與速度v之間關系的部分數據如下表:
速度v(千米/小時) | …… | 5 | 10 | 20 | 32 | 40 | 48 | …… |
流量q(輛/小時) | …… | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | …… |
(1)根據上表信息,下列三個函數關系式中,刻畫q,v關系最準確的是___________.(只填上正確答案的序號)
①q=90v+100;②q=![]() ;③q=2v2+120v.
;③q=2v2+120v.
(2)請利用(1)中選取的函數關系式分析,當該路段的車流速度為多少時,流量達到最大?最大流量是多少?
(3)已知q,v,k滿足q=vk,請結合(1)中選取的函數關系式繼續解決下列問題.
①市交通運行監控平臺顯示,當18≤v≤28該路段不會出現交通擁堵現象.試分析當車流密度k在什么范圍時,該路段不會出現交通擁堵現象;
②在理想狀態下,假設前后兩車車頭之間的距離d(米)均相等,當d=25米時請求出此時的速度v.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,二次函數![]() (其中
(其中![]() ,
,![]() 是常數,
是常數,![]() 為正整數)
為正整數)
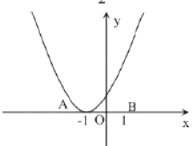
(1)若![]() 經過點
經過點![]() 求
求![]() 的值.
的值.
(2)當![]() ,若
,若![]() 與
與![]() 軸有公共點時且公共點的橫坐標為非零的整數,確定
軸有公共點時且公共點的橫坐標為非零的整數,確定![]() 的值;
的值;
(3)在(2)的條件下將![]() 的圖象向下平移
的圖象向下平移![]() 個單位,得到函數圖象
個單位,得到函數圖象![]() ,求
,求![]() 的解析式;
的解析式;
(4)在(3)的條件下,將![]() 的圖象在
的圖象在![]() 軸下方的部分沿
軸下方的部分沿![]() 軸翻折,圖象的其余部分保持不變,得到一個新的圖象
軸翻折,圖象的其余部分保持不變,得到一個新的圖象![]() ,請結合新的圖象解答問題,若直線
,請結合新的圖象解答問題,若直線![]() 與
與![]() 有兩個公共點時,請直接寫出
有兩個公共點時,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果連鎖店銷售某種熱帶水果,其進價為20元/千克.銷售一段時間后發現:該水果的日銷量![]() (千克)與售價
(千克)與售價![]() (元/千克)的函數關系如圖所示:
(元/千克)的函數關系如圖所示:
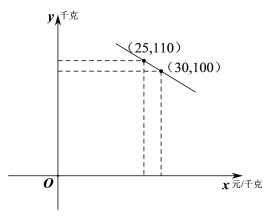
(1)求![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(2)當售價為多少元/千克時,當日銷售利潤最大,最大利潤為多少元?
(3)由于某種原因,該水果進價提高了![]() 元/千克(
元/千克(![]() ),物價局規定該水果的售價不得超過40元/千克,該連鎖店在今后的銷售中,日銷售量與售價仍然滿足(1)中的函數關系.若日銷售最大利潤是
),物價局規定該水果的售價不得超過40元/千克,該連鎖店在今后的銷售中,日銷售量與售價仍然滿足(1)中的函數關系.若日銷售最大利潤是![]() 元,請直接寫出
元,請直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=3cm,BC=4cm,P、Q兩點同時從點C出發,點P沿從![]() 的方向運動,速度為2cm/秒;點Q沿從
的方向運動,速度為2cm/秒;點Q沿從![]() 的方向運動,速度為1cm/秒.當運動時間為t秒﹙0≤t≤3.5﹚時,設△PCQ的面積為y(cm2)(當P、Q兩點未開始運動時,△PCQ的面積為0).則y(cm2)和t﹙秒﹚的函數關系的圖象大致是( )
的方向運動,速度為1cm/秒.當運動時間為t秒﹙0≤t≤3.5﹚時,設△PCQ的面積為y(cm2)(當P、Q兩點未開始運動時,△PCQ的面積為0).則y(cm2)和t﹙秒﹚的函數關系的圖象大致是( )

A.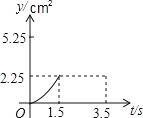 B.
B.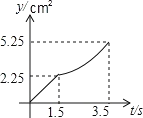 C.
C.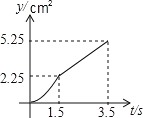 D.
D.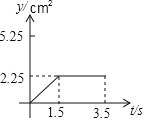
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知以△ABC的BC邊上一點O為圓心的圓,經過A,B兩點,且與BC邊交于點E,D為弧BE的中點,連接AD交OE于點F,若AC=FC
(Ⅰ)求證:AC是⊙O的切線;
(Ⅱ)若BF=5,DF=![]() ,求⊙O的半徑.
,求⊙O的半徑.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為配合全市“禁止焚燒秸稈”工作,某學校舉行了“禁止焚燒秸稈,保護環境,從我做起”為主題的演講比賽. 賽后組委會整理參賽同學的成績,并制作了如下不完整的頻數分布表和頻數分布直方圖.
分數段(分數為x分) | 頻數 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x<90 | 16 | b% |
90≤x<100 | 4 | 10% |
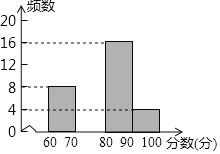
請根據圖表提供的信息,解答下列問題:
(1)表中的a= ,b= ;請補全頻數分布直方圖;
(2)若用扇形統計圖來描述成績分布情況,則分數段70≤x<80對應扇形的圓心角的度數是 ;
(3)競賽成績不低于90分的4名同學中正好有2名男同學,2名女同學. 學校從這4名同學中隨機抽2名同學接受電視臺記者采訪,則正好抽到一名男同學和一名女同學的概率為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市在黨中央實施“精準扶貧”政策的號召下,大力開展科技扶貧工作,幫助農民組建農副產品銷售公司,某農副產品的年產量不超過100萬件,該產品的生產費用y(萬元)與年產量x(萬件)之間的函數圖象是頂點為原點的拋物線的一部分(如圖①所示);該產品的銷售單價z(元/件)與年銷售量x(萬件)之間的函數圖象是如圖②所示的一條線段,生產出的產品都能在當年銷售完,達到產銷平衡,所獲毛利潤為w萬元.(毛利潤=銷售額﹣生產費用)

(1)請直接寫出y與x以及z與x之間的函數關系式;
(2)求w與x之間的函數關系式;并求年產量多少萬件時,所獲毛利潤最大?最大毛利潤是多少?
(3)由于受資金的影響,今年投入生產的費用不會超過360萬元,今年最多可獲得多少萬元的毛利潤?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com