
【題目】如圖,拋物線y=ax2+bx﹣2的對稱軸是直線x=1,與x軸交于A,B兩點,與y軸交于點C,點A的坐標為(﹣2,0),點P為拋物線上的一個動點,過點P作PD⊥x軸于點D,交直線BC于點E.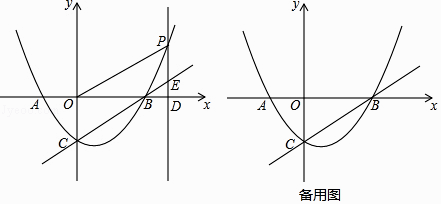
(1)求拋物線解析式;
(2)若點P在第一象限內,當OD=4PE時,求四邊形POBE的面積;
(3)在(2)的條件下,若點M為直線BC上一點,點N為平面直角坐標系內一點,是否存在這樣的點M和點N,使得以點B,D,M,N為頂點的四邊形是菱形?若存在上,直接寫出點N的坐標;若不存在,請說明理由.
【答案】
(1)
解:∵拋物線y=ax2+bx﹣2的對稱軸是直線x=1,A(﹣2,0)在拋物線上,∴ 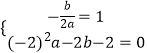 ,解得:
,解得: 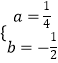 ,拋物線解析式為y=
,拋物線解析式為y= ![]() x2﹣
x2﹣ ![]() x﹣2;
x﹣2;
(2)
解:令y= ![]() x2﹣
x2﹣ ![]() x﹣2=0,解得:x1=﹣2,x2=4,當x=0時,y=﹣2,∴B(4,0),C(0,﹣2),設BC的解析式為y=kx+b,則
x﹣2=0,解得:x1=﹣2,x2=4,當x=0時,y=﹣2,∴B(4,0),C(0,﹣2),設BC的解析式為y=kx+b,則 ![]() ,解得:
,解得: 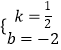 ,∴y=
,∴y= ![]() x﹣2,
x﹣2,
設D(m,0),
∵DP∥y軸,
∴E(m, ![]() m﹣2),P(m,
m﹣2),P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),
m﹣2),
∵OD=4PE,
∴m=4( ![]() m2﹣
m2﹣ ![]() m﹣2﹣
m﹣2﹣ ![]() m+2),
m+2),
∴m=5,m=0(舍去),
∴D(5,0),P(5, ![]() ),E(5,
),E(5, ![]() ),
),
∴四邊形POBE的面積=S△OPD﹣S△EBD= ![]() ×5×
×5× ![]() ﹣
﹣ ![]() 1×
1× ![]() =
= ![]() ;
;
(3)
解:存在,設M(n, ![]() n﹣2),
n﹣2),
①以BD為對角線,如圖1,
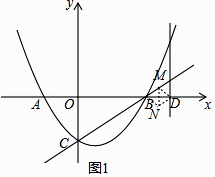
∵四邊形BNDM是菱形,
∴MN垂直平分BD,
∴n=4+ ![]() ,
,
∴M( ![]() ,
, ![]() ),
),
∵M,N關于x軸對稱,
∴N( ![]() ,﹣
,﹣ ![]() );
);
②以BD為邊,如圖2,
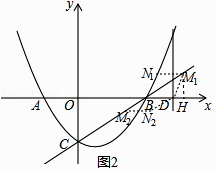
∵四邊形BNDM是菱形,
∴MN∥BD,MN=BD=MD=1,
過M作MH⊥x軸于H,
∴MH2+DH2=DM2,
即( ![]() n﹣2)2+(n﹣5)2=12,
n﹣2)2+(n﹣5)2=12,
∴n1=4(不合題意),n2=5.6,
∴N(4.6, ![]() ),
),
同理( ![]() n﹣2)2+(4﹣n)2=1,
n﹣2)2+(4﹣n)2=1,
∴n1=4+ ![]() (不合題意,舍去),n2=4﹣
(不合題意,舍去),n2=4﹣ ![]() ,
,
∴N(5﹣ ![]() ,
, ![]() ),
),
③以BD為邊,如圖3,

過M作MH⊥x軸于H,
∴MH2+BH2=BM2,
即( ![]() n﹣2)2+(n﹣4)2=12,
n﹣2)2+(n﹣4)2=12,
∴n1=4+ ![]() ,n2=4﹣
,n2=4﹣ ![]() (不合題意,舍去),
(不合題意,舍去),
∴N(5+ ![]() ,
, ![]() ),
),
綜上所述,當N( ![]() ,﹣
,﹣ ![]() )或(4.6,
)或(4.6, ![]() )或(5﹣
)或(5﹣ ![]() ,
, ![]() )或(5+
)或(5+ ![]() ,
, ![]() ),以點B,D,M,N為頂點的四邊形是菱形.
),以點B,D,M,N為頂點的四邊形是菱形.
【解析】(1)由拋物線y=ax2+bx﹣2的對稱軸是直線x=1,A(﹣2,0)在拋物線上,于是列方程即可得到結論;(2)根據函數解析式得到B(4,0),C(0,﹣2),求得BC的解析式為y= ![]() x﹣2,設D(m,0),得到E(m,
x﹣2,設D(m,0),得到E(m, ![]() m﹣2),P(m,
m﹣2),P(m, ![]() m2﹣
m2﹣ ![]() m﹣2),根據已知條件列方程得到m=5,m=0(舍去),求得D(5,0),P(5,
m﹣2),根據已知條件列方程得到m=5,m=0(舍去),求得D(5,0),P(5, ![]() ),E(5,
),E(5, ![]() ),根據三角形的面積公式即可得到結論;(3)設M(n,
),根據三角形的面積公式即可得到結論;(3)設M(n, ![]() n﹣2),①以BD為對角線,根據菱形的性質得到MN垂直平分BD,求得n=4+
n﹣2),①以BD為對角線,根據菱形的性質得到MN垂直平分BD,求得n=4+ ![]() ,于是得到N(
,于是得到N( ![]() ,﹣
,﹣ ![]() );②以BD為邊,根據菱形的性質得到MN∥BD,MN=BD=MD=1,過M作MH⊥x軸于H,根據勾股定理列方程即可得到結論.
);②以BD為邊,根據菱形的性質得到MN∥BD,MN=BD=MD=1,過M作MH⊥x軸于H,根據勾股定理列方程即可得到結論.


 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:初中數學 來源: 題型:
【題目】如圖①,點O是直線AB上的一點,∠COD是直角,OE平分∠BOC.
(1)如圖①,若∠AOC=40°,求∠DOE的度數;
(2)如圖①,若∠AOC=α,直接寫出∠DOE的度數(用含α的代數式表示)
(3)將圖①中的∠COD繞頂點O順時針旋轉至圖②的位置,OE平分∠BOC.
①探究∠AOC和∠DOE的度數之間的關系,寫出你的結論,并說明理由;
②在∠AOC的內部有一條射線OF,且∠AOC﹣3∠AOF=2∠BOE,試確定∠AOF與∠DOE的度數之間的關系,說明理由.
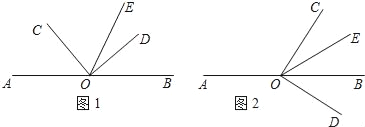
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一般情況下![]() 不成立,但有些數可以使得它成立,例如:m=n=0時,我們稱使得
不成立,但有些數可以使得它成立,例如:m=n=0時,我們稱使得![]() 成立的一對數m,n為“相伴數對”,記為(m,n).
成立的一對數m,n為“相伴數對”,記為(m,n).
(1)若(m,1)是“相伴數對”,則m=_____;
(2)(m,n)是“相伴數對”,則代數式![]() m﹣[n+
m﹣[n+![]() (6﹣12n﹣15m)]的值為_____.
(6﹣12n﹣15m)]的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線y1=x+1與雙曲線![]() (k>0)相交于點A、B,已知點A坐標(2,m).
(k>0)相交于點A、B,已知點A坐標(2,m).
(1)求k的值;
(2)求點B的坐標,并觀察圖象,寫出當![]() 時,x的取值范圍.
時,x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2+bx+c(a≠0)與x軸交于點A(﹣1,0)和B(3,0),與y軸交于點C,點D的橫坐標為m(0<m<3),連結DC并延長至E,使得CE=CD,連結BE,BC.
(1)求拋物線的解析式;
(2)用含m的代數式表示點E的坐標,并求出點E縱坐標的范圍;
(3)求△BCE的面積最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,用火柴棒擺出一列正方形圖案,第①個圖案用了 4 根,第②個圖案用了 12 根,第③個圖案用了 24 根,按照這種方式擺下去,擺出第⑥個圖案用火柴棒的根數是( )

A. 84 B. 81 C. 78 D. 76
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:矩形ABCD中,AB=2,BC=5,E、P分別在AD、BC上,且DE=BP=1.

(1)判斷△BEC的形狀,并說明理由?
(2)判斷四邊形EFPH是什么特殊四邊形?并證明你的判斷;
(3)求四邊形EFPH的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
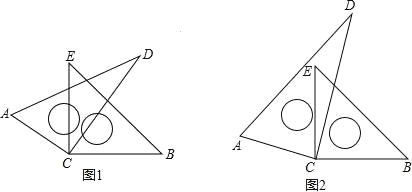
【題目】如圖,將一副直角三角尺的直角頂點C疊放在一起.
(1)如圖 1,若 CE 恰好是∠ACD 的角平分線,請你猜想此時 CD 是不是∠ECB 的角平分線?只回答出“是”或“不是”即可;
(2)如圖 2,若∠ECD=α,CD 在∠BCE 的內部,請你猜想∠ACE 與∠DCB是否相等?并簡述理由;
(3)在(2)的條件下,請問∠ECD 與∠ACB 的和是多少?并簡述理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com