【題目】如圖，正方形ABCD邊長為2，E為CD的中點，以點A為中心，把△ADE順時針旋轉90°得△ABF，連接EF，則EF的長等于 ． 
【答案】
【解析】解：根據旋轉的性質得到：BF=DE=1，在直角△EFC中：EC=DC﹣DE=1，CF=BC+BF=3．
根據勾股定理得到：EF= 
= ．
所以答案是： ．
【考點精析】解答此題的關鍵在于理解正方形的性質的相關知識，掌握正方形四個角都是直角，四條邊都相等；正方形的兩條對角線相等，并且互相垂直平分，每條對角線平分一組對角；正方形的一條對角線把正方形分成兩個全等的等腰直角三角形；正方形的對角線與邊的夾角是45o；正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形，以及對旋轉的性質的理解，了解①旋轉后對應的線段長短不變，旋轉角度大小不變；②旋轉后對應的點到旋轉到旋轉中心的距離不變；③旋轉后物體或圖形不變，只是位置變了．
輕巧奪冠周測月考直通中考系列答案科目：初中數學 來源： 題型：
【題目】若一個三位數，其個位數加上十位數等于百位數，可表示為t=100（x+y）+10y+x，則稱實數t為“加成數”，將t的百位作為個位，個位作為十位，十位作為百位，組成一個新的三位數h．規定q=t﹣h，f（m）=
，例如：321是一個“加成數”，將其百位作為個位，個位作為十位，十位作為百位，得到的數h=213，∴q=321﹣213=108，f（m）=
=12．
（1）當f（m）最小時，求此時對應的“加成數”的值；
（2）若f（m）是24的倍數，則稱f（m）是“節氣數”，猜想這樣的“節氣數”有多少個，并求出所有的“節氣數”．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】王師傅常用角尺平分一個角，如圖所示，學生小明可用三角尺平分一個角，他們在∠AOB兩邊上分別取OM、ON，使OM＝ON，前者使角尺兩邊相同刻度分別與M、N重合，角尺頂點為P；后者分別過M、N作OA、OB的垂線，交點為P，則均可得到△OMP≌△ONP，其依據分別是____________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，點M，N分別在AB，BC上，將△BMN沿MN翻折得到△FMN，若MF∥AD，FN∥DC，則∠D的度數為( )
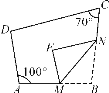
A. 115° B. 105° C. 95° D. 85°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線y=﹣x2+bx+c與x軸交于A（1，0），B（﹣3，0）兩點．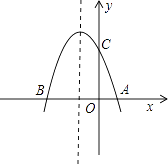
（1）求該拋物線的解析式；
（2）設（1）中的拋物線交y軸與C點，在該拋物線的對稱軸上是否存在點Q，使得△QAC的周長最小？若存在，求出Q點的坐標；若不存在，請說明理由；
（3）在（1）中的拋物線上的第二象限上是否存在一點P，使△PBC的面積最大？若存在，求出點P的坐標及△PBC的面積最大值；若沒有，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，直線a經過正方形ABCD的頂點A，分別過正方形的頂點B、D作BF⊥a于點F，DE⊥a于點E，若DE=8，BF=5，則EF的長為__．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠B＝∠C，AB＝10 cm，BC＝8 cm，D為AB的中點，點P在線段上以3 cm/s的速度由點B向點C運動，同時，點Q在線段CA上以相同速度由點C向點A運動，一個點到達終點后另一個點也停止運動．當△BPD與△CQP全等時，求點P運動的時間．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在矩形ABCD中，對角線AC，BD交于點E，DF⊥AC于F點，若∠ADF=3∠FDC，則∠DEC的度數是（ ）
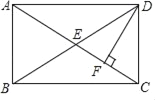
A. 30° B. 45° C. 50° D. 55°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知如圖1，在以O為原點的平面直角坐標系中，拋物線y= 
x2+bx+c與x軸交于A、B兩點，與y軸交于點C（0，﹣1），連接AC，AO=2CO，直線l過點G（0，t）且平行于x軸，t＜﹣1，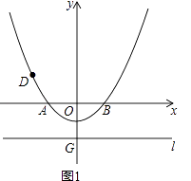
（1）求拋物線對應的二次函數的解析式；
（2）若D為拋物線y= x2+bx+c上一動點，是否存在直線l使得點D到直線l的距離與OD的長恒相等？若存在，求出此時t的值；
（3）如圖2，若E、F為上述拋物線上的兩個動點，且EF=8，線段EF的中點為M，求點M縱坐標的最小值．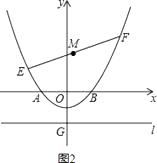
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com