
【題目】在△ABC中,AB=AC,點D是直線BC上一點(不與B,C重合),以AD為一邊在AD的右側作△ADE,使AD=AE,∠DAE=∠BAC,連結CE.

(1)如圖1,當點D在線段BC上時,如果∠BAC=90°,則∠BCE= °.
(2)設∠BAC=α,∠BCE=β.
①如圖2,當點D在線段BC上移動時,α,β之間有怎樣的數量關系?請說明理由.
②當點D在直線BC上移動時,α,β之間有怎樣的數量關系?請你在備用圖上畫出圖形,并直接寫出你的結論.
【答案】(1)90°;(2)①α+β=180°,見解析;②見解析,α=β
【解析】
(1)先用等式的性質得出∠CAE=∠BAD,進而得出△ABD≌△ACE,有∠B=∠ACE,最后用等式的性質即可得出結論;
(2)①由(1)的結論即可得出α+β=180°;②同(1)的方法即可得出結論.
解:(1)∵∠DAE=∠BAC,∠BAC=∠BAD+∠DAC=∠EAC+∠DAC;
∴∠CAE=∠BAD;
在△ABD和△ACE中,
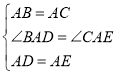
∴△ABD≌△ACE(SAS);
∴∠B=∠ACE;
∴∠BCE=∠BCA+∠ACE=∠BCA+∠B=180°﹣∠BAC=90°;
故答案為90°;
(2)①由(1)中可知β=180°﹣α,
∴α、β存在的數量關系為α+β=180°;
②當點D在射線BC上時,如圖1,
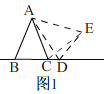
同(1)的方法即可得出,△ABD≌△ACE(SAS);
∴∠ABD=∠ACE,
∴β=∠BCE=∠ACB+∠ACE=∠ACB+∠ABD=180°﹣∠BAC=180°﹣α,
∴α+β=180°;
當點D在射線BC的反向延長線上時,如圖2,
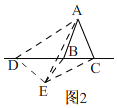
同(1)的方法即可得出,△ABD≌△ACE(SAS);
∴∠ABD=∠ACE,
∴β=∠BCE=∠ACE﹣∠ACB=∠ABD﹣∠ACB=∠BAC=α,
∴α=β.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD⊥BC,BE⊥AC,垂足分別為點D、E,AD與BE交于點F,BF=AC, ∠ABE=22°,則∠CAD的度數是________°.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是作一個角的角平分線的方法:以![]() 的頂點
的頂點![]() 為圓心,以任意長為半徑畫弧,分別交
為圓心,以任意長為半徑畫弧,分別交![]() 于
于![]() 兩點,再分別以
兩點,再分別以![]() 為圓心,大于
為圓心,大于![]() 長為半徑作畫弧,兩條弧交于點
長為半徑作畫弧,兩條弧交于點![]() ,作射線
,作射線![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() .
.

(1)若![]() ,求
,求![]() 的度數;
的度數;
(2)若![]() ,垂足為
,垂足為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行于x軸的直線AC分別交函數 y![]() =x
=x![]() (x≥0)與 y
(x≥0)與 y![]() =
= ![]() x
x![]() (x≥0)的圖象于 B,C兩點,過點C作y軸的平行線交y
(x≥0)的圖象于 B,C兩點,過點C作y軸的平行線交y![]() =x
=x![]() (x≥0)的圖象于點D,直線DE∥AC交 y
(x≥0)的圖象于點D,直線DE∥AC交 y![]() =
=![]() x
x![]() (x≥0)的圖象于點E,則
(x≥0)的圖象于點E,則![]() =( )
=( )

A. ![]() B. 1 C.
B. 1 C. ![]() D. 3﹣
D. 3﹣ ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖象交x軸于(-1,0)點,則下列結論中正確的是( )
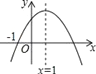
A. c<0 B. a-b+c<0 C. b2<4ac D. 2a+b=0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com