Question

如下圖，已知△ABC中，∠C＝90°，AC＝4，BC＝3，DE∥AB，交AC于D，交BC于E，CF⊥DE于F，DE在△ABC內作平行運動，問DE為何值時，△ADE的面積最大，并求出這個最大值．

Answer 1

答案：
解析：

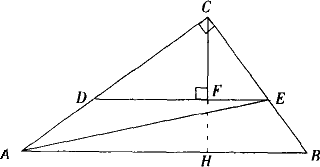
　　簡解：延長CF交AB于H．

　　易求得AB＝5，CH＝．

　　設FH＝x，則CF＝－x．

　　∵DE∥AB．

　　∴＝

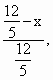
　　∴DE＝5－x．

　　又設△ADE的面積為y，于是

　　y＝DE·FH＝(5－x)·x

　　＝－x²＋x

　　＝－(x－)²＋(0＜x＜)．

　　∴當x＝，即DE＝時，△ADE的面積最大，最大值為．

　　分析：DE作為△ADE的底，延長CF交AB于H，可得到△ADE的高FH，通過設未知數建立等式向函數轉化．

　　簡評：幾何問題向函數轉化，函數的最大值發揮了決定的作用．

　　綜上，解決幾何最值問題，可直接考慮應用幾何中的公里、定理，如線段最短公里、垂線段最短、角的不等關系等；或考慮取線段、點的極端位置，然后通過計算求最值；或把幾何問題代數比，向方程、不等式、函數轉化，用代數法求最值．解題時要根據題目特點具體分析，靈活掌握．