
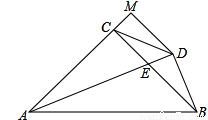
如圖,△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC于M,連CD,下列結論:①AC+CE=AB;②BD=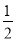 AE;③∠CDA=45°;④
AE;③∠CDA=45°;④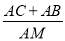 為定值,其中正確的有( )個。
為定值,其中正確的有( )個。
A、1 B、2 C、3 D、4
D.
【解析】
試題分析:過E作EQ⊥AB于Q,
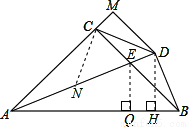
∵∠ACB=90°,AE平分∠CAB,
∴CE=EQ,
∵∠ACB=90°,AC=BC,
∴∠CBA=∠CAB=45°,
∵EQ⊥AB,
∴∠EQA=∠EQB=90°,
由勾股定理得:AC=AQ,
∴∠QEB=45°=∠CBA,
∴EQ=BQ,
∴AB=AQ+BQ=AC+CE,∴①正確;
作∠ACN=∠BCD,交AD于N,
∵∠CAD=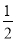 ∠CAB=22.5°=∠BAD,
∠CAB=22.5°=∠BAD,
∴∠DBA=90°-22.5°=67.5°,
∴∠DBC=67.5°-45°=22.5°=∠CAD,
∴∠DBC=∠CAD,
∵AC=BC,∠ACN=∠DCB,
∴△ACN≌△BCD,
∴CN=CD,
∵∠ACN+∠NCE=90°,
∴∠NCB+∠BCD=90°,
∴∠CND=∠CDN=45°,
∴∠ACN=45°-22.5°=22.5°=∠CAN,
∴AN=CN,
∴∠NCE=∠AEC=67.5°,
∴CN=NE,
∴CD=AN=EN=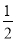 AE,
AE,
∴②正確,③正確;
過D作DH⊥AB于H,
∵∠MCD=∠CAD+∠CDA=67.5°,
∠DBA=90°-∠DAB=67.5°,
∴∠MCD=∠DBA,
∵AE平分∠CAB,DM⊥AC,DH⊥AB,
∴DM=DH,
在△DCM和△DBH中
∠M=∠DHB=90°,∠MCD=∠DBA,DM=DH,
∴△DCM≌△DBH,
∴BH=CM,
由勾股定理得:AM=AH,
∴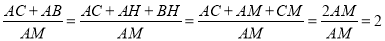 ,
,
∴④正確;
故選D.
考點:1.等腰直角三角形;2.三角形內角和外角性質;3.全等三角形的判定與性質;4.直角三角形斜邊上的中線.


 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案科目:初中數學 來源:2014-2015學年江蘇東臺許河鎮中學七年級上學期第二次月檢數學試卷(解析版) 題型:選擇題
下列各組數中,數值相等的是( ).
A.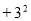 與
與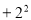 B.
B.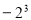 與
與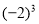
C.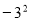 與
與 D.
D.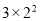 與
與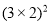
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省黃石市八年級9月月考數學試卷(解析版) 題型:解答題
如圖,已知AM∥BN,AC平分∠MAB,BC平分∠NBA。
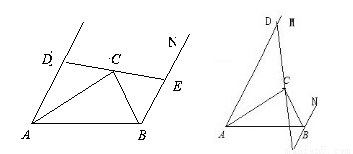
(1)過點C作直線DE,分別交AM、BN于點D、E,則AB、AD、BE三條線的長度之間存在何種等量關系?請直接寫出關系式 。
(2)如圖,若將直線DE繞點C轉動,使DE與AM交于點D,與NB的延長線交于點E,則AB、AD、BE三條線的長度之間存在何種等量關系?請你給出結論并加以證明。
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省黃石市八年級9月月考數學試卷(解析版) 題型:填空題
如圖,小亮從A點出發,沿直線前進10米后向左轉30°,再沿直線前進10米,又向左轉30°,……照這樣走下去,他第一次回到出發地A點時,一共走了__________米

查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省黃石市八年級9月月考數學試卷(解析版) 題型:選擇題
如圖,已知MB=ND,∠MBA=∠NDC,下列條件中不能判定△ABM≌△CDN的是( )

A、∠M=∠N B、 AM∥CN C、AB=CD D、AM=CN
查看答案和解析>>
科目:初中數學 來源:2014-2015學年貴州省安順市七年級上學期期末檢測數學試卷(解析版) 題型:解答題
先化簡,再求值:5(3a2b-ab2)-4(-ab2+3a2b), 其中a=-1,b=-2.(8分)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年黑龍江省哈爾濱市道里區九年級上學期期末調研測試數學試卷(解析版) 題型:解答題
(本題7分) 圖l、圖2分別是7×6的網格,網格中的每個小正方形的邊長均為1,點A、B在小正方形的頂點上.請在網格中按照下列要求畫出圖形:
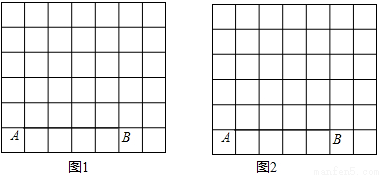
(1)在圖1中以AB為邊作四邊形ABCD (點C、D在小正方形的頂點上),使得四邊形ABCD中心對稱圖形,且△ABD為軸對稱圖形(畫出一個即可);
(2)在圖2中以AB為邊作四邊形ABEF (點E、F在小正方形的頂點上),使得四邊形ABEF中心對稱圖形
但不是軸對稱圖形,且tan∠FAB=3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com