已知一平面內的任意四點,其中任何三點都不在一條直線上,試問:是否一定能從這樣的四點中選出三點構成一個三角形,使得這個三角形至少有一內角不大于45°?請證明你的結論.
【答案】
分析:結論是以疑問形式出現的,不妨先假定是肯定的,然后推理.若推出矛盾,則說明結論是否定的;若推不出矛盾,則可考慮去證明結論是肯定的.
解答: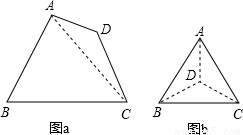
證明:能.
(1)如圖a,若四點A,B,C,D構成凸四邊形.則必有一個內角≤90°.不妨設為∠A.
這是因為,假設四個內角都大于90°,則360°=∠A+∠B+∠C+∠D>4×90°=360°.矛盾.
則∠BAC+∠CAD≤90°.
則∠BAC與∠CAD中必有一個≤

×90°=45°.
故結論成立.
(2)如圖b.若四點A,B,C,D構成四邊形.則△ABC中必有一個內角≤

×180°=60°.
不防設∠A≤60°.
又∠A=∠BAD+∠CAD≤60°.
則∠BAD與∠CAD值中必有一個≤

×60°<45°.
故結論成立.
點評:本題結合角的比較考查反證法,解此題關鍵要懂得反證法的意義及步驟.
反證法的步驟是:(1)假設結論不成立;
(2)從假設出發(fā)推出矛盾;
(3)假設不成立,則結論成立.
在假設結論不成立時要注意考慮結論的反面所有可能的情況,如果只有一種,那么否定一種就可以了,如果有多種情況,則必須一一否定.

 證明:能.
證明:能. ×90°=45°.
×90°=45°. ×180°=60°.
×180°=60°. ×60°<45°.
×60°<45°.

 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案
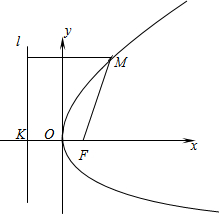 先閱讀短文,再回答短文后面的問題.
先閱讀短文,再回答短文后面的問題.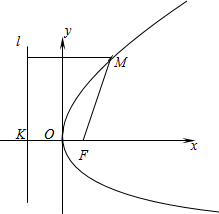 先閱讀短文,再回答短文后面的問題.
先閱讀短文,再回答短文后面的問題. ,0),準線l的方程為x=-
,0),準線l的方程為x=- .
.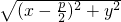 ,d=|x+
,d=|x+ |∴
|∴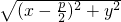 =|x+
=|x+ |
| ,0),它的準線方程是x=-
,0),它的準線方程是x=- .
.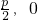 )
)
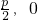 )
)
 )
)
 )
)
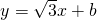 經過拋物線y2=4x的焦點,與拋物線相交于兩點A、B,求線段AB的長.
經過拋物線y2=4x的焦點,與拋物線相交于兩點A、B,求線段AB的長.