
【題目】如圖1,P 為△ABC 內一點,連接 PA、PB、PC,在△PAB、△PBC 和△PAC 中,如果存在一個三角形與△ABC 相似,那么就稱 P 為△ABC 的自相似點.
(1)如圖 2,已知 Rt△ABC 中,∠ACB=90°,CD 是 AB 上的中線,過點 B 作 BE⊥CD,垂足為 E,試說明 E 是△ABC 的自相似點.
(2)如圖 3,在△ABC 中,∠A<∠B<∠C.若△ABC 的三個內角平分線的交 點 P 是該 三角形的自相似點,求該三角形三個內角的度數.

【答案】(1)詳見解析;(2)![]()
【解析】
(1)根據已知條件得出∠BEC=∠ACB,以及∠BCE=∠ABC,得出△BCE∽△ABC,即可得出結論;
(2)根據∠PBC=∠A,∠BCP=∠ABC=∠2∠PBC=2∠A,∠ACB=2∠BCP=4∠A,即可得出各內角的度數.
解:(1)在Rt△ABC中,∠ACB=90°,CD是AB上的中線,
∴CD=![]() AB,
AB,
∴CD=BD,
∴∠BCE=∠ABC,
∵BE⊥CD,∴∠BEC=90°,
∴∠BEC=∠ACB,
∴△BCE∽△ABC,
∴E是△ABC的自相似點;
(2)∵P是△ABC的內心,∴∠PBC=![]() ∠ABC,∠PCB=
∠ABC,∠PCB=![]() ∠ACB,
∠ACB,
∵△ABC的內心P是該三角形的自相似點,
∴△BCP∽△ABC
∴∠PBC=∠A,∠BCP=∠ABC=2∠PBC=2∠A,∠ACB=2∠BCP=4∠A,
∴∠A+2∠A+4∠A=180°,
∴∠A=![]() ,
,
∴該三角形三個內角度數為:![]() ,
,![]() ,
,![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2+2x+3與x軸相交于A、B兩點(點A在點B的左側),與y軸相交于點C,頂點為D.
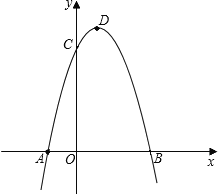
(1)直接寫出A、B、C三點的坐標和拋物線的對稱軸;
(2)連接BC,與拋物線的對稱軸交于點E,點P為線段BC上的一個動點,過點P作PF∥DE交拋物線于點F,設點P的橫坐標為m;
①用含m的代數式表示線段PF的長,并求出當m為何值時,四邊形PEDF為平行四邊形?
②設△BCF的面積為S,求S與m的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分別為E,F.
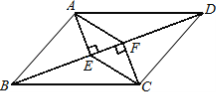
(1)求證:△ABE≌△CDF;
(2)若AC與BD交于點O,求證:AO=CO.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB與直線CD相交于點O,EO⊥AB,OF平分∠AOC,
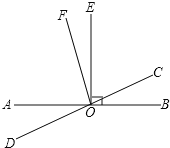
(1)請寫出∠EOC的余角 ;
(2)若∠BOC=40°,求∠EOF的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】[知識背景]:
數軸上,點A,B表示的數為a,b,則A,B兩點的距離AB=|a﹣b|,A、B的中點P表示的數為![]() .
.
[知識運用]:
已知式子(a+4)x3+2x2﹣x+3是關于x的二次三項式,且二次項系數為b,且a,b在數軸上對應的點分別為A,B(如圖1),解答下列問題:
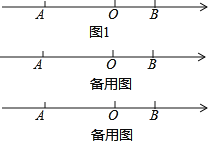
(1)a= ,b= ,AB= ;
(2)若點A以每秒2個單位的長度沿數軸向右運動,t秒后到達原點O,求t的值;
(3)若點A,B都以每秒2個單位長度的速度沿數軸向右運動到達點M和點N,而O點不動,經過t秒后,M,O,N三點中,其中一點是另外兩點的中點,求此時t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩支“徒步隊”到野外沿相同路線徒步,徒步的路程為24千米.甲隊步行速度為4千米/時,乙隊步行速度為6千米/時.甲隊出發1小時后,乙隊才出發,同時乙隊派一名聯絡員跑步在兩隊之間來回進行一次聯絡(不停頓),他跑步的速度為10千米/時.
(1)乙隊追上甲隊需要多長時間?
(2)聯絡員從出發到與甲隊聯系上后返回乙隊時,他跑步的總路程是多少?
(3)從甲隊出發開始到乙隊完成徒步路程時止,何時兩隊間間隔的路程為1千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列每一列數,按規律填空
(1)![]() , ,……
, ,……
(2)![]() , ,……
, ,……
(3)![]() , ,……
, ,……
(4)在(1)列數中第100個數是 ,在(2)列數中第200個數是 ,在(3)列數中第199個數是 。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com