
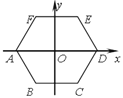
【題目】如圖,正六邊形 ABCDEF的中心與坐標原點O重合,其中A(-2,0).將六邊形 ABCDEF繞原點O按順時針方向旋轉2018次,每次旋轉60°,則旋轉后點A的對應點A'的坐標是( ).
A. (1,![]() ) B. (
) B. (![]() ,1) C. (1,
,1) C. (1,![]() ) D. (-1,
) D. (-1,![]() )
)
 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:初中數學 來源: 題型:
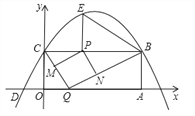
【題目】如圖,矩形OABC的兩邊在坐標軸上,點A的坐標為(10,0),拋物線y=ax2+bx+4過點B,C兩點,且與x軸的一個交點為D(﹣2,0),點P是線段CB上的動點,設CP=t(0<t<10).
(1)請直接寫出B、C兩點的坐標及拋物線的解析式;
(2)過點P作PE⊥BC,交拋物線于點E,連接BE,當t為何值時,∠PBE=∠OCD?
(3)點Q是x軸上的動點,過點P作PM∥BQ,交CQ于點M,作PN∥CQ,交BQ于點N,當四邊形PMQN為正方形時,請求出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,△ABC中,∠ACB=90°,AC=BC,點E是BC上一點,連接AE.
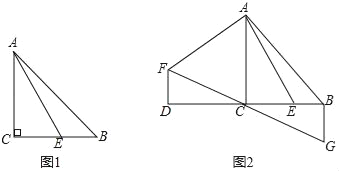
(1)如圖1,當∠BAE=15°,CE=![]() 時,求AB的長.
時,求AB的長.
(2)如圖2,延長BC至D,使DC=BC,將線段AE繞點A順時針旋轉90°得線段AF,連接DF,過點B作BG⊥BC,交FC的延長線于點G,求證:BG=BE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據閱讀材料,解決問題.
數n是一個三位數,各數位上的數字互不相同,且都不為零,從它各數位上的數字中任選兩個構成一個兩位數,這樣就可以得到六個不同的兩位數,我們把這六個不同的兩位數叫做數n的“生成數”.數n的所有“生成數”之和與22的商記為G(n),例如n=123,它的六個“生成數”是12,13,21,23,31,32,這六個“生成數”的和12+13+21+23+31+32=132,132÷22=6,所以G(123)=6.
(1)計算:G(125),G(746);
(2)數s,t是兩個三位數,它們都有“生成數”,a,1,4分別是s的百位、十位、個位上的數字,x,y,6分別是t的百位、十位、個位上的數字,規定:k=![]() ,若G(s)G(t)=84,求k的最小值.
,若G(s)G(t)=84,求k的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
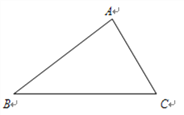
【題目】如圖,在△ABC中,∠A=80°,∠B=40°.
(1)求作線段BC的垂直平分線DE,垂足為E,交AB于點D;(要求;尺規作圖,保留作圖痕跡,不寫作法)
(2)在(1)的條件下,連接CD,求證:AC=CD.
查看答案和解析>>
科目:初中數學 來源: 題型:
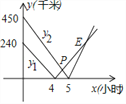
【題目】在一條筆直的高速公路上依次有3個標志點A、B、C,甲、乙兩車分別從A、C兩點同時出發,勻速行駛,甲車從A→B→C,乙車從C→B→A,甲、乙兩車離B的距離y1、y2(千米)與行駛時間x(小時)之間的函數關系圖象如圖所示.觀察圖象,給出下列結論:①A、C之間的路程為690千米;②乙車比甲車每小時快30千米;③4.5小時兩車相遇;④點E的橫坐標表示兩車第二次相遇的時間;⑤點E的坐標為(7,180)其中正確的有________(把所有正確結論的序號都填在橫線上).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解全校學生下學期參加社區活動的情況,學校隨機調查了本校50名學生參加社區活動的次數,并將調查所得的數據整理如下:
活動次數x | 頻數 | 頻率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | m | b |
12<x≤15 | 4 | 0.08 |
15<x≤18 | 2 | n |

根據以上圖表信息,解答下列問題:
(1)表中a=___,b=___;
(2)請把頻數分布直方圖補充完整(畫圖后請標注相應的數據);
(3)若該校共有1500名學生,請估計該校在下學期參加社區活動超過6次的學生有多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com