
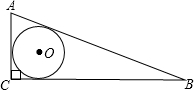
 某焊工要在一兩直角邊為30cm、40cm的直角三角形鐵片中割出一個圓,要使所剩廢料最少?請幫他描出該圓,并求出此時圓的半徑.
某焊工要在一兩直角邊為30cm、40cm的直角三角形鐵片中割出一個圓,要使所剩廢料最少?請幫他描出該圓,并求出此時圓的半徑.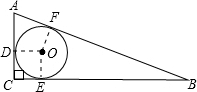 解:由勾股定理得:AB=
解:由勾股定理得:AB= =50cm
=50cm

科目:初中數學 來源:2008年湖南省婁底市雙峰縣中考數學模擬試卷(解析版) 題型:解答題
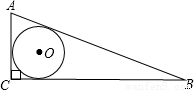
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com