
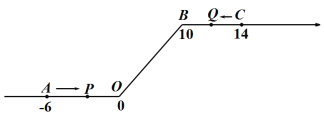
【題目】如圖,將一條數軸在原點O和點B處各折一下,得到一條“折線數軸”.圖中點A表示﹣6,點B表示10,點C表示14,我們稱點A和點C在數軸上相距20個長度單位.動點P從點A出發,以2單位/秒的速度沿著“折線數軸”的正方向運動,從點O運動到點B期間速度變為原來的一半,之后立刻恢復原速;同時,動點Q從點C出發,以1單位/秒的速度沿著數軸的負方向運動,從點B運動到點O期間速度變為原來的兩倍,之后也立刻恢復原速.設運動的時間為t秒.
問:
(1)動點P從點A運動至C點需要時間為 秒;P、Q兩點相遇時,求出相遇點M所對應的數是 ;
(2)求當t為何值時,P、O兩點在數軸上相距的長度與Q、B兩點在數軸上相距的長度相等.
【答案】(1)15;4(2)t的值為2、3.5或5.
【解析】
(1)根據路程除以速度等于時,可得答案;根據相遇時P,Q的時間相等,可得方程,解出即可.
(2)根據PO與BQ的時間相等,可得方程,解出即可.
(1)點P運動至點C時,所需時間t=6÷2+10÷1+4÷2=15(s),
答:動點P從點A運動至C點需要15秒;
由題可知,P、Q兩點相遇在線段OB上于M處,設OM=x.
則6÷2+x÷1=4÷1+(10-x)÷2,
x=4,
答:M所對應的數為4.
(2)P點運動完時間:6÷2+10÷1+4÷2=15(s)
Q點運動完時間:4÷1+10÷2+6÷1=15(s)
P、O兩點在數軸上相距的長度與Q、B兩點在數軸上相距的長度相等有以下可能:
①動點Q在CB上,動點P在AO上,
則:4-1t=6-2t,解得:t=2.
②動點Q在CB上,動點P在OB上,
則:4-1t=1×(t-3),解得:t=3.5.
③動點Q在BO上,動點P在OB上,
則:2(t-4)=1×(t-3),解得:t=5.
④動點Q在OA上,動點P在OB上,
則:1×(t-9)+10=1×(t-3),無解
④動點Q在OA上,動點P在BC上,
則:1×(t-9)+10=2×(t-13)+10,解得:t=17>15,
綜上所述:t的值為2、3.5或5.


科目:初中數學 來源: 題型:
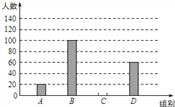
【題目】國家規定“中小學生每天在校體育活動時間不低于1小時”.為此,我區就“你每天在校體育活動時間是多少”的問題隨機調查了區內300名初中學生.根據調查結果繪制成的統計圖(部分)如圖所示,其中分組情況是:
A組:t<0.5h B組:0.5h≤t<1h C組:1h≤t<1.5h D組:t≥1.5h
請根據上述信息解答下列問題:
(1)C組的人數是 .
(2)本次調查數據的中位數落在 組內;
(3)若我區有5400名初中學生,請你估計其中達國家規定體育活動時間的人約有多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個整數能表示成a2+b2(a、b是正整數)的形式,則稱這個數為“完美數”。例如5是“完美數”,因為5=22+12,再如M=x2+2xy+2y2=(x+y)2 +y2(x、y是正整數),所以M也是“完美數”。
(1)請你再寫一個小于10的“完美數”,并判斷29是否為“完美數”;
(2)試判斷(x2+9y2)(4y2+x2)(x、y是正整數)是否為“完美數”,并說明理由;
(3)已知S=x2+4y2+4x-12y+k(x、y是正整數,k是常數),要使S為“完美數”,試求出符合條件的一個k值,并說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一個多位自然數的任意兩個相鄰數位上,左邊數位上的數總比右邊數位上的數小1,那么我們把這樣的自然數叫做“相連數”,例如:234,4567,56789,......都是“相連數”.
(1)請直接寫出最大的兩位“相連數”與最小的三位“相連數”,并求它們的和;
(2)若某個“相連數”恰好等于其個位數的576倍,求這個“相連數”.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某天,一蔬菜經營戶用114元從蔬菜批發市場購進黃瓜和土豆共40kg到菜市場去賣,黃瓜和土豆這天的批發價好零售價(單位:元/kg)如下表所示:
品名 | 批發價 | 零售價 |
黃瓜 | 2.4 | 4 |
土豆 | 3 | 5 |
(1)他當天購進黃瓜和土豆各多少千克?
(2)如果黃瓜和土豆全部賣完,他能賺多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分8分)
為了加強學生課外閱讀,開闊視野,某校開展了“書香校園,從我做起”的主題活動.學校隨機抽取了部分學生,對他們一周的課外閱讀時間進行調查,繪制出頻數分布表和頻數分布直方圖的一部分如下:


請根據圖表信息回答下列問題:
(1)頻數分布表中的![]() ,
,![]() ;
;
(2)將頻數分布直方圖補充完整;
(3)學校將每周課外閱讀時間在![]() 小時以上的學生評為“閱讀之星”,請你估計該校
小時以上的學生評為“閱讀之星”,請你估計該校![]() 名學生中評為“閱讀之星”的有多少人?
名學生中評為“閱讀之星”的有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
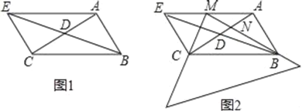
【題目】已知:如圖1,Rt△ABC中,∠BAC=90°,點D是線段AC的中點,連接BD并延長至點E,使BE=2BD.連接AE,CE.
(1)求證:四邊形ABCE是平行四邊形;
(2)如圖2所示,將三角板頂點M放在AE邊上,兩條直角邊分別過點B和點C,若∠MEC=∠EMC,BM交AC于點N.求證:△ABN≌△MCN.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com