
【題目】如圖1,在等腰Rt△ABC中,∠BAC=90°,點E在AC上(且不與點A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,連接AD,分別以AB,AD為鄰邊作平行四邊形ABFD,連接AF.
(1)求證:△AEF是等腰直角三角形;
(2)如圖2,將△CED繞點C逆時針旋轉,當點E在線段BC上時,連接AE,求證:AF=![]() AE;
AE;
(3)如圖3,將△CED繞點C繼續逆時針旋轉,當平行四邊形ABFD為菱形,且△CED在△ABC的下方時,若AB=2![]() ,CE=2,求線段AE的長.
,CE=2,求線段AE的長.

【答案】(1)答案見解析;(2)答案見解析;(3)4![]() .
.
【解析】試題分析:(1)依據AE=EF,∠DEC=∠AEF=90°,即可證明△AEF是等腰直角三角形;
(2)連接EF,DF交BC于K,先證明△EKF≌△EDA,再證明△AEF是等腰直角三角形即可得出結論;
(3)當AD=AC=AB時,四邊形ABFD是菱形,先求得EH=DH=CH=![]() ,Rt△ACH中,AH=3
,Rt△ACH中,AH=3![]() ,即可得到AE=AH+EH=4
,即可得到AE=AH+EH=4![]() .
.
試題解析:解:(1)如圖1.∵四邊形ABFD是平行四邊形,∴AB=DF.∵AB=AC,∴AC=DF.∵DE=EC,∴AE=EF.∵∠DEC=∠AEF=90°,∴△AEF是等腰直角三角形;
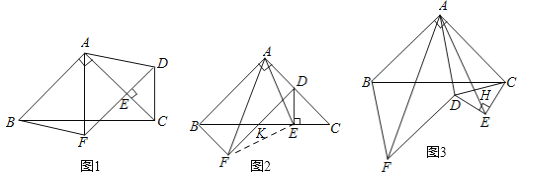
(2)如圖2,連接EF,DF交BC于K.∵四邊形ABFD是平行四邊形,∴AB∥DF,∴∠DKE=∠ABC=45°,∴∠EKF=180°﹣∠DKE=135°,EK=ED.∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,∴∠EKF=∠ADE.∵∠DKC=∠C,∴DK=DC.∵DF=AB=AC,∴KF=AD.在△EKF和△EDA中, 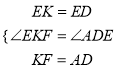 ,∴△EKF≌△EDA(SAS),∴EF=EA,∠KEF=∠AED,∴∠FEA=∠BED=90°,∴△AEF是等腰直角三角形,∴AF=
,∴△EKF≌△EDA(SAS),∴EF=EA,∠KEF=∠AED,∴∠FEA=∠BED=90°,∴△AEF是等腰直角三角形,∴AF=![]() AE.
AE.
(3)如圖3,當AD=AC=AB時,四邊形ABFD是菱形,設AE交CD于H,依據AD=AC,ED=EC,可得AE垂直平分CD,而CE=2,∴EH=DH=CH=![]() ,Rt△ACH中,AH=
,Rt△ACH中,AH=![]() =3
=3![]() ,∴AE=AH+EH=4
,∴AE=AH+EH=4![]() .
.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:初中數學 來源: 題型:
【題目】已知某電腦公司有A型,B型,C型三種型號的電腦,其價格分別為A型每臺6000元,B型每臺4000元,C型每臺2500元 ,某市實驗中學計劃將100500元錢全部用于從該電腦公司購進電腦共36臺
(1)若全部購進的是兩種不同型號的電腦,請你設計出幾種不同的購買方案方案供該校選擇,并說出理由;
(2)能否同時購進三種型號的電腦,若能,請設計出購買方案;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用描點法畫出函數y=![]() 的圖象,并回答下列問題:
的圖象,并回答下列問題:
(1)當x=-3時, y=_________.
(2)當1≤x≤4時,y的取值范圍是_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖,![]() 三點在同一直線上,
三點在同一直線上,![]() .
.
(1)已知點![]() 在直線
在直線![]() 上,根據條件,請補充完整圖形,并求
上,根據條件,請補充完整圖形,并求![]() 的長;
的長;
![]()
(2)已知點![]() 在直線
在直線![]() 上,
上,![]() 分別是
分別是![]() ,
,![]() 的中點,根據條件,請補充完整圖形,并求
的中點,根據條件,請補充完整圖形,并求![]() 的長,直接寫出
的長,直接寫出![]() 與
與![]() 的長存在的數量關系;
的長存在的數量關系;
![]()
(3)已知點![]() 在直線
在直線![]() 上,
上,![]() 分別是
分別是![]() ,
,![]() 的中點,根據條件,請補充完整圖形,并求
的中點,根據條件,請補充完整圖形,并求![]() 的長,直接寫出
的長,直接寫出![]() 與
與![]() 的長存在的數量關系.
的長存在的數量關系.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】嘉淇準備完成題目:化簡:![]() ,發現系數“
,發現系數“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,請你化簡:(3x2+6x+8)–(6x+5x2+2);
”猜成3,請你化簡:(3x2+6x+8)–(6x+5x2+2);
(2)他媽媽說:“你猜錯了,我看到該題標準答案的結果是常數.”通過計算說明原題中“![]() ”是幾?
”是幾?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某河流受暴雨影響,水位不斷上漲,下面是某天此河流的水位記錄:
時間(時) | 0 | 4 | 8 | 12 | 16 | 20 | 24 |
水位(米) | 2 | 2.5 | 3 | 4 | 5 | 6 | 8 |
(1)上表反映的是哪兩個量之間的關系?自變量和因變量各是什么?
(2)根據表格畫了表示兩個變量的折線統計圖.
(3)哪段時間水位上升得最快?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A、B兩倉庫分別有水泥20噸和30噸,C、D兩工地分別需要水泥15噸和35噸.已知從A、B倉庫到C、D工地的運價如下表:
到C工地 | 到D工地 | |
A倉庫 | 每噸15元 | 每噸12元 |
B倉庫 | 每噸10元 | 每噸9元 |
(1)若從A倉庫運到C工地的水泥為![]() 噸,則用含x的代數式表示從A倉庫運到D工地的水泥為 噸,從B倉庫將水泥運到D工地的運輸費用為 元;
噸,則用含x的代數式表示從A倉庫運到D工地的水泥為 噸,從B倉庫將水泥運到D工地的運輸費用為 元;
(2)求把全部水泥從A、B兩倉庫運到C、D兩工地的總運輸費(用含![]() 的代數式表示并化簡);
的代數式表示并化簡);
(3)如果從A倉庫運到C工地的水泥為15噸時,那么總運輸費為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:數x、y、z中較大的數稱為max{x,y,z}.例如max{﹣3,1,﹣2}=1,函數y=max{﹣t+4,t,![]() }表示對于給定的t的值,代數式﹣t+4,t,
}表示對于給定的t的值,代數式﹣t+4,t,![]() 中值最大的數,如當t=1時y=3,當t=0.5時,y=6.則當t=_________時函數y的值最小.
中值最大的數,如當t=1時y=3,當t=0.5時,y=6.則當t=_________時函數y的值最小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數軸上從左到右有![]() 三個點,點
三個點,點![]() 對應的數是10,
對應的數是10,![]() .
.
(1)點![]() 對應的數是________,點
對應的數是________,點![]() 對應的數是________.
對應的數是________.
(2)若數軸上有一點![]() ,且
,且![]() ,則點
,則點![]() 表示的數是什么?
表示的數是什么?
(3)動點![]() 從
從![]() 出發,以每秒4個單位長度的速度向終點
出發,以每秒4個單位長度的速度向終點![]() 移動,同時,動點
移動,同時,動點![]() 從點
從點![]() 出發,以每秒1個單位長度的速度向終點
出發,以每秒1個單位長度的速度向終點![]() 移動,設移動時間為
移動,設移動時間為![]() 秒. 當點
秒. 當點![]() 和點
和點![]() 間的距離為8個單位長度時,求
間的距離為8個單位長度時,求![]() 的值.
的值.
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com