
【題目】如圖,二次函數y=a(x2+2mx﹣3m2)(其中a,m是常數a<0,m>0)的圖象與x軸分別交于A、B(點A位于點B的右側),與y軸交于點C(0,3),點D在二次函數的圖象上,CD∥AB,連結AD.過點A作射線AE交二次函數的圖象于點E,AB平分∠DAE.
(1)求a與m的關系式;
(2)求證:![]() 為定值;
為定值;
(3)設該二次函數的圖象的頂點為F.探索:在x軸的正半軸上是否存在點G,連結GF,以線段GF、AD、AE的長度為三邊長的三角形是直角三角形?如果存在,只要找出一個滿足要求的點G即可,并用含m的代數式表示該點的橫坐標;如果不存在,請說明理由.
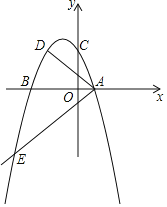
【答案】(1)am2=﹣1;(2)證明見解析;(3)存在,點G的橫坐標為3m.
【解析】
(1)將點C的坐標代入拋物線表達式,即可求解;
(2)證明RtADM△∽Rt△ANE,求出點E(x,![]() ),將點E的坐標代入拋物線表達式,得到E(﹣4m,﹣5),即可求解;
),將點E的坐標代入拋物線表達式,得到E(﹣4m,﹣5),即可求解;
(3)求出點F(﹣m,4),得到直線FC的表達式,求出點G(3m,0),即可求解.
解:(1)將點C的坐標代入拋物線表達式得:﹣3am2=3,
解得:am2=﹣1;
(2)對于二次函數y=a(x2+2mx﹣3m2),令y=0,則x=m或﹣3m,
∴函數的對稱軸為:x=﹣m,
∵CD∥AB,
∴點D、C的縱坐標相同,故點D(﹣2m,3),
故點A、B的坐標分別為:(m,0)、(﹣3m,0),
設點E(x,y),y=a(x2+2mx﹣3m2),
分別過點D、E作x軸的垂線,垂足分別為M、N,
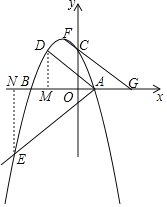
∵AB平分∠DAE,
∴∠DAM=∠EAN,
∴RtADM△∽Rt△ANE,
∴![]() ,即
,即![]() ,
,
解得:y=![]() ,
,
故點E(x,![]() ),
),
將點E的坐標代入拋物線表達式并解得:x=﹣4m,
則y=![]() =﹣5,
=﹣5,
故點E(﹣4m,﹣5),
故![]() =
=![]() =
=![]() 為定值;
為定值;
(3)存在,理由:
函數的對稱軸為x=﹣m,當x=﹣m時,y=a(x2+2mx﹣3m2)=4,即點F(﹣m,4),
由點F、C的坐標得,直線FC的表達式為:y=﹣![]() x+3,令y=0,則x=3m,即點G(3m,0),
x+3,令y=0,則x=3m,即點G(3m,0),
GF2=(3m+m)2+42=16m2+16,
同理AD2=9m2+9,AE2=25m2+25,
故AE2=AD2+GF2,
GF、AD、AE的長度為三邊長的三角形是直角三角形,
點G的橫坐標為3m.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:初中數學 來源: 題型:
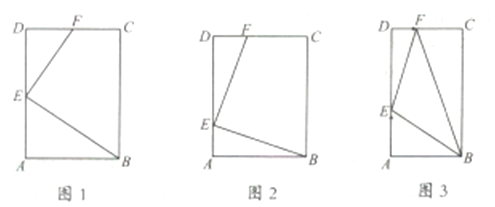
【題目】矩形![]() 中,
中,![]() (其中
(其中![]() )
)
(1)點![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上,
上,![]() ;
;
①如圖![]() ,若
,若![]() ,且點
,且點![]() 是
是![]() 中點,求證
中點,求證![]() ;
;
②如圖![]() ,若
,若![]() ,且
,且![]() ,求證:
,求證:![]() ;
;
(2)如圖![]() ,當
,當![]() ,
,![]() 時,點
時,點![]() 以
以![]() 的速度從
的速度從![]() 到
到![]() ,點
,點![]() 以
以![]() 的速度從
的速度從![]() 到
到![]() ,當點
,當點![]() 到
到![]() 時兩點都停止運動,則點
時兩點都停止運動,則點![]() 的運動時間
的運動時間![]() 為多少時,
為多少時,![]() 的面積
的面積![]() 最小,最小面積為多少?
最小,最小面積為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有甲、乙兩家草莓采摘園,草莓的銷售價格相間,在生長旺季,兩家均排出優惠方案.甲園的優惠方案是:采摘的草莓不超過![]() 時,按原價銷售;若超過
時,按原價銷售;若超過![]() 超過部分
超過部分![]() 折優惠;乙園的優惠方案是:游客進園需購買
折優惠;乙園的優惠方案是:游客進園需購買![]() 元門票.采摘的草莓直接按降價出售.已知在甲園、乙園采摘草莓
元門票.采摘的草莓直接按降價出售.已知在甲園、乙園采摘草莓![]() 時,所需費用相同.
時,所需費用相同.
在乙采摘園所需費用![]() ( 元)與草梅采摘量
( 元)與草梅采摘量![]() (千克)滿足一次函數關系,如下表:
(千克)滿足一次函數關系,如下表:
數量 |
|
|
|
| ··· |
費用 |
|
|
|
| ··· |
(1)求![]() 與
與![]() 的函數關系式(不必寫出
的函數關系式(不必寫出![]() 的范圍);
的范圍);
(2)求兩個采摘園的草莓在生長旺季前的銷售價格.并求在甲采摘園所需費用![]() (元)與草莓采摘量
(元)與草莓采摘量![]() (千克)的函數關系式
(千克)的函數關系式![]() ;
;
(3)若嘉琪準備花費![]() 元去采摘草莓,去哪個園采摘,可以得到更多數量的草莓? 說明理由.
元去采摘草莓,去哪個園采摘,可以得到更多數量的草莓? 說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
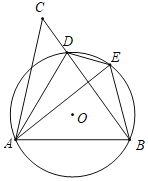
【題目】如圖,D是△ABC的BC邊上一點,連接AD,作△ABD的外接圓,將△ADC沿直線AD折疊,點C的對應點E落在⊙O上.
(1)求證:AE=AB.
(2)填空:
①當∠CAB=90°,cos∠ADB=![]() ,BE=2時,邊BC的長為 .
,BE=2時,邊BC的長為 .
②當∠BAE= 時,四邊形AOED是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,創新小組要測量公園內一棵樹的高度AB,其中一名小組成員站在距離樹10米的點E處,測得樹頂A的仰角為54°.已知測角儀的架高CE=1.8米,則這顆樹的高度為_________米.(結果保留一位小數.參考數據:sin54°=0.8090,cos54°=0.5878,tan54°=1.3764)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司計劃購買A,B兩種型號的機器人搬運材料.已知A型機器人比B型機器人每小時多搬運30kg材料,且A型機器人搬運1000kg材料所用的時間與B型機器人搬運800kg材料所用的時間相同.
(1)求A,B兩種型號的機器人每小時分別搬運多少材料;
(2)該公司計劃采購A,B兩種型號的機器人共20臺,要求每小時搬運材料不得少于2800kg,則至少購進A型機器人多少臺?
查看答案和解析>>
科目:初中數學 來源: 題型:
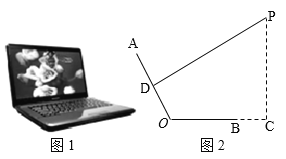
【題目】如圖1是一臺放置在水平桌面上的筆記本電腦,將其側面抽象成如圖2所示的幾何圖形.若顯示屏AO與鍵盤BO長均為24cm,點P為眼睛所在位置,D為AO的中點,連接PD,且PD⊥AO(此時點P為最佳視角),點C在OB的延長線上,PC⊥BC,BC=12cm.
(1)當PA=45cm時,求PC的長;
(2)當∠AOC=115°時,線段PC的長比(1)中線段PC的長是增大還是減小?請通過計算說明.(結果精確到0.1cm,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com