
【題目】溫州享有“中國筆都”之稱,其產品暢銷全球,某制筆企業欲將n件產品運往A,B,C三地銷售,要求運往C地的件數是運往A地件數的2倍,各地的運費如圖所示.設安排x件產品運往A地. 
(1)當n=200時,①根據信息填表:
A地 | B地 | C地 | 合計 | |
產品件數(件) | x | 2x | 200 | |
運費(元) | 30x |
②若運往B地的件數不多于運往C地的件數,總運費不超過4000元,則有哪幾種運輸方案?
(2)若總運費為5800元,求n的最小值.
【答案】
(1)解:①根據信息填表
A地 | B地 | C地 | 合計 | |
產品件數(件) | 200﹣3x | |||
運費 | 1600﹣24x | 50x | 56x+1600 |
②由題意,得 ![]() ,
,
解得40≤x≤42 ![]() ,
,
∵x為正整數,
∴x=40或41或42,
∴有三種方案,分別是(i)A地40件,B地80件,C地80件;
(ii)A地41件,B地77件,C地82件;
(iii)A地42件,B地74件,C地84件
(2)解:由題意,得30x+8(n﹣3x)+50x=5800,
整理,得n=725﹣7x.
∵n﹣3x≥0,
∴725﹣7x﹣3x≥0,
∴﹣10x≥﹣725,
∴x≤72.5,
又∵x≥0,
∴0≤x≤72.5且x為正整數.
∵n隨x的增大而減少,
∴當x=72時,n有最小值為221
【解析】(1)①運往B地的產品件數=總件數n﹣運往A地的產品件數﹣運往B地的產品件數;運費=相應件數×一件產品的運費; ②根據運往B地的件數不多于運往C地的件數,總運費不超過4000元列出不等式組,求得正整數解的個數即可;(2)總運費=A產品的運費+B產品的運費+C產品的運費,進而根據函數的增減性及(1)中②得到的x的取值求得n的最小值即可.
【考點精析】關于本題考查的一元一次不等式組的應用,需要了解1、審:分析題意,找出不等關系;2、設:設未知數;3、列:列出不等式組;4、解:解不等式組;5、檢驗:從不等式組的解集中找出符合題意的答案;6、答:寫出問題答案才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】請在圖中補全坐標系及缺失的部分,并在橫線上寫恰當的內容.圖中各點坐標如下:A(1,0),B(6,0),C(1,3),D(6,2).線段AB上有一點M,使△ACM∽△BDM,且相似比不等于1.求出點M的坐標并證明你的結論.
M( , )
證明:∵CA⊥AB,DB⊥AB
∴∠CAM=∠DBM=度.
∵CA=AM=3,DB=BM=2
∴∠ACM=∠AMC(),∠BDM=∠BMD(同理),
∴∠ACM= ![]() (180°﹣)=45°.∠BDM=45°(同理).
(180°﹣)=45°.∠BDM=45°(同理).
∴∠ACM=∠BDM
在△ACM與△BDM中,
∠CAM=∠DBM
∴△ACM∽△BDM(如果一個三角形的兩個角與另一個三角形的兩個角對應相等,那么這兩個三角形相似)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在方格紙中,每個小方格都是邊長為1cm的正方形,△ABC的三個頂點都在格點上,將△ABC繞點O逆時針旋轉90°后得到△A′B′C′(其中A、B、C的對應點分別為A′,B′,C′,則點B在旋轉過程中所經過的路線的長是cm.(結果保留π)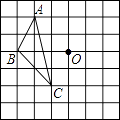
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地植物園從正門到側門有一條小路,甲徒步從正門出發勻速走向側門,乙與甲同時出發,騎自行車從側門勻速前往正門到達正門后休息0.2小時,然后按原路原速勻速返回側門,圖中折線分別表示甲、乙到側門的距離y(km)與出發時間x(h)之間的函數關系圖象,根據圖象信息解答下列問題:
(1)求甲到側門的距離y與x之間的函數關系式;
(2)求甲、乙第一次相遇時到側門的距離.
(3)求甲、乙第二次相遇的時間.
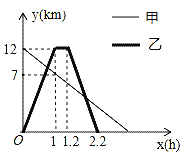
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知動點A在函數 ![]() 的圖象上,AB⊥x軸于點B,AC⊥y軸于點C,延長CA至點D,使AD=AB,延長BA至點E,使AE=AC.直線DE分別交x,y軸分別于點P,Q.當QE:DP=4:9時,圖中陰影部分的面積等于 .
的圖象上,AB⊥x軸于點B,AC⊥y軸于點C,延長CA至點D,使AD=AB,延長BA至點E,使AE=AC.直線DE分別交x,y軸分別于點P,Q.當QE:DP=4:9時,圖中陰影部分的面積等于 . 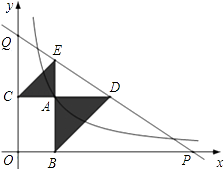
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,為測量江兩岸碼頭B、D之間的距離,從山坡上高度為50米的A處測得碼頭B的仰角∠EAB為15°,碼頭D的仰角∠EAD為45°,點C在線段BD的延長線上,AC⊥BC,垂足為C,求碼頭B、D的距離(結果保留整數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,扇形DOE的半徑為3,邊長為 ![]() 的菱形OABC的頂點A,C,B分別在OD,OE,
的菱形OABC的頂點A,C,B分別在OD,OE, ![]() 上,若把扇形DOE圍成一個圓錐,則此圓錐的高為( )
上,若把扇形DOE圍成一個圓錐,則此圓錐的高為( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在矩形ABCD中,AB=a,BC=b,點E是線段AD邊上的任意一點(不含端點A、D),連結BE、CE.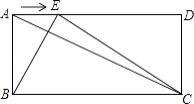
(1)若a=5,sin∠ACB= ![]() ,求b.
,求b.
(2)若a=5,b=10當BE⊥AC時,求出此時AE的長.
(3)設AE=x,試探索點E在線段AD上運動過程中,使得△ABE與△BCE相似時,求a、b應滿足什么條件,并求出此時x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知矩形ABCD,AB=6,BC=8,E,F分別是AB,BC的中點,AF與DE相交于I,與BD相交于H,則四邊形BEIH的面積為( )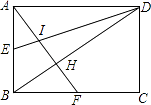
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com