
【題目】在同一條道路上,甲車從![]() 地到
地到![]() 地,乙車從
地,乙車從![]() 地到
地到![]() 地,兩車同時出發以各自速度勻速行駛. 兩車相遇后,乙車休息了
地,兩車同時出發以各自速度勻速行駛. 兩車相遇后,乙車休息了![]() 小時,然后繼續原速駛往
小時,然后繼續原速駛往![]() 地,圖中的折線段表示甲、乙兩車之間的距離
地,圖中的折線段表示甲、乙兩車之間的距離![]() (千米)與行駛時間
(千米)與行駛時間![]() (小時)的函數關系的圖象,下列說法錯誤的是( )
(小時)的函數關系的圖象,下列說法錯誤的是( )
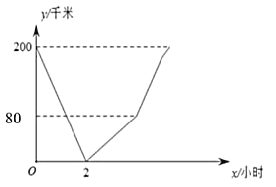
A.甲乙兩車出發![]() 小時后相遇B.甲車速度是
小時后相遇B.甲車速度是![]() 千米/小時
千米/小時
C.甲車到![]() 地比乙車到
地比乙車到![]() 地早
地早![]() D.相遇時乙車距離
D.相遇時乙車距離![]() 地
地![]() 千米
千米
【答案】C
【解析】
根據相遇時距離為0,即甲乙兩車出發2小時后相遇可求得甲乙兩車的速度和,根據第二段圖像為甲車單獨出發2小時的圖象可求得甲車的速度,進而求得乙車的速度,進而分析得出答案.
解:∵出發2h后,其距離為零,即兩車相遇,
∴選項A說法正確;
∵甲的速度為:80÷2=40(km/h),
∴選項B說法正確;
∵甲乙兩車的速度和為:200÷2=100(km/h),
∴乙車的速度為:100﹣40=60(km/h),
∴甲的總時間為:200÷40=5(h),
乙的總時間為:200÷60+2=5![]() (h)
(h)
∵5![]() ﹣5=
﹣5=![]() (h)=20(min)
(h)=20(min)
∴選項C說法錯誤;
∵2×40=80(km),
∴選項D說法正確;
故選:C.


科目:初中數學 來源: 題型:
【題目】現有![]() 四張不透明的卡片,除正面上的圖案不同外,其他均相同,將這四張卡片背 面向上洗勻后放在桌面上.
四張不透明的卡片,除正面上的圖案不同外,其他均相同,將這四張卡片背 面向上洗勻后放在桌面上.
(1)從中隨機取出一張卡片,卡片上的圖案是中心對稱圖形的概率是_____;
(2)若從四張卡片中隨機拿出兩張卡片,請用畫樹狀圖或列表的方法,求抽取的兩張卡片都是軸對稱圖形的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校計劃購進甲、乙兩種規格的書架,經市場調查發現有線上和線下兩種購買方式,具體情況如下表:
規格 | 線下 | 線上 | ||
單價(元/個) | 運費(元/個) | 單價(元/個) | 運費(元/個) | |
甲 | 240 | 0 | 210 | 20 |
乙 | 300 | 0 | 250 | 30 |
(1)如果在線下購買甲、乙兩種書架共30個,花費8280元,求甲、乙兩種書架各購買了多少個?
(2)如果在線上購買甲、乙兩種書架共30個,且購買乙種書架的數量不少于甲種書架的3倍,請求出花費最少的購買方案及花費.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線![]() 與
與![]() 軸和
軸和![]() 軸分別交于點
軸分別交于點![]() 和點
和點![]() 拋物線
拋物線![]() 經過點
經過點![]() 與直線
與直線![]() 的另一個交點為
的另一個交點為![]() .
.
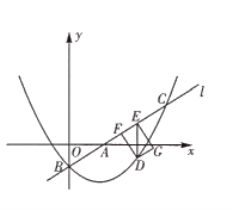
![]() 求
求![]() 的值和拋物線的解析式
的值和拋物線的解析式
![]() 點
點![]() 在拋物線上,
在拋物線上,![]() 軸交直線
軸交直線![]() 于點
于點![]() 點
點![]() 在直線
在直線![]() 上,且四邊形
上,且四邊形![]() 為矩形.設點
為矩形.設點![]() 的橫坐標為
的橫坐標為![]() 矩形
矩形![]() 的周長為
的周長為![]() 求
求![]() 與
與![]() 的函數關系式以及
的函數關系式以及![]() 的最大值
的最大值
![]() 將
將![]() 繞平面內某點
繞平面內某點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() (點
(點![]() 分別與
分別與![]() 點對應),若
點對應),若![]() 的兩個頂點恰好落在拋物線上,請直接寫出點
的兩個頂點恰好落在拋物線上,請直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
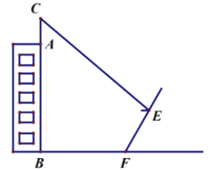
【題目】如圖,某校有一教學樓![]() ,其上有一避雷針
,其上有一避雷針![]() 為
為![]() 米,教學樓后面有一小山,其坡度為
米,教學樓后面有一小山,其坡度為![]() 山坡上有一休息亭
山坡上有一休息亭![]() 供爬山人員休息,測得山坡腳
供爬山人員休息,測得山坡腳![]() 與教學摟的水平距離
與教學摟的水平距離![]() 為
為![]() 米,與休息亭的距離
米,與休息亭的距離![]() 為
為![]() 米,從休息亭
米,從休息亭![]() 測得教學樓上避雷針頂點
測得教學樓上避雷針頂點![]() 的仰角為
的仰角為![]() ,求教學摟
,求教學摟![]() 的高度.(結果保留根號)(注:坡度
的高度.(結果保留根號)(注:坡度![]() 是指坡面的鉛直高度與水平寬度的比)
是指坡面的鉛直高度與水平寬度的比)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年10月10日傍晚18:10左右,江蘇省無錫市山區312國道上海方向K135處,錫港路上跨橋出現橋面側翻,造成3人死亡,2人受傷,盡管該事故原因初步分析為半掛牽引車嚴重超載導致橋梁發生側翻,但是也引起了社會各界對橋梁設計安全性的擔憂,我市積極開展對橋梁結構設計的安全性進行評估(已知:抗傾覆系數越高,安全性越強;當抗傾覆系數≥2.5時,認為該結構安全),現在重慶市隨機抽取了甲、乙兩個設計院,對其各自在建的或已建的20座橋梁項目進行排查,將得到的抗傾覆數據進行整理、描述和分析(抗傾覆數據用x表示,共分成6組:A.0≤x<2.5,B.2.5≤x<5.0,C.5.0≤x<7.5,D.7.5≤x<10.0,E.10.0≤x<12.5,F.12.5≤x<15),下面給出了部分信息;
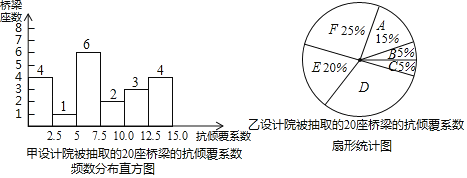
其中,甲設計院C組的抗傾覆系數是:7,7,7,6,7,7;
乙設計院D組的抗傾覆系數是:8,8,9,8,8,8;
甲、乙設計院分別被抽取的20座橋梁的抗傾覆系數統計表
設計院 | 甲 | 乙 |
平均數 | 7.7 | 8.9 |
眾數 | a | 8 |
中位數 | 7 | b |
方差 | 19.7 | 18.3 |
根據以上信息解答下列問題:
(1)扇形統計圖中D組數據所對應的圓心角是 度,a= ,b= ;
(2)根據以上數據,甲、乙兩個設計院中哪個設計院的橋梁安全性更高,說明理由(一條即可): ;
(3)據統計,2018年至2019年,甲設計院完成設計80座橋梁,乙設計院完成設計120座橋梁,請估算2018年至2019年兩設計院的不安全橋梁的總數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以矩形ABCD對角線AC為底邊作等腰直角△ACE,連接BE,分別交AD,AC于點F,N,CD=AF,AM平分∠BAN.下列結論:①EF⊥ED;②∠BCM=∠NCM;③AC=![]() EM;④BN2+EF2=EN2;⑤AEAM=NEFM,其中正確結論的個數是( )
EM;④BN2+EF2=EN2;⑤AEAM=NEFM,其中正確結論的個數是( )
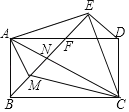
A.2B.3C.4D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種型號油電混合動力汽車,從A地到B地燃油行駛純燃油費用76元,從A地到B地用電行駛純電費用26元,已知每行駛1千米,純燃油費用比純用電費用多0.5元.
(1)求每行駛1千米純用電的費用;
(2)若要使從A地到B地油電混合行駛所需的油、電費用合計不超過39元,則至少用電行駛多少千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,矩形![]() 的頂點
的頂點![]() ,
,![]() 分別在
分別在![]() 軸、
軸、![]() 軸上,對角線
軸上,對角線![]() 軸,反比例函數
軸,反比例函數![]() 的圖象經過矩形對角線的交點
的圖象經過矩形對角線的交點![]() ,若點
,若點![]() ,
,![]() ,則
,則![]() 的值為__________.
的值為__________.
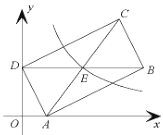
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com