Question

如圖，AB是半圓O的直徑，且AB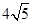＝，矩形CDEF內(nèi)接于半圓，點C，D在AB上，點E，F在半圓上．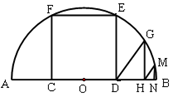

（1）當矩形CDEF相鄰兩邊FC︰CD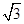＝︰2時，求弧AF的度數(shù)；
（2）當四邊形CDEF是正方形時：
①試求正方形CDEF的邊長；
②若點G，M在⊙O上， GH⊥AB于H，MN⊥AB于N，且△GDH和△MHN都是等腰直角三角形，求HN的長．  

Answer 1

（1）弧AF的度數(shù)為60°（2）①4 ②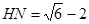

解析試題分析：（1）連結(jié)FO，根據(jù)圓的對稱性，矩形CDEF內(nèi)接于半圓可得CO＝OD，
∴R t△COF中，FC︰CD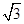＝︰1，∴∠FOC=60°
∴弧AF的度數(shù)為60°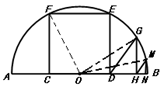

（2）① ∵四邊形CDEF是正方形，∴FC=2CO
∵FC²＋CO²=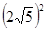，解得CO＝2，∴CF＝4，正方形的邊長為4
② 連結(jié)OG，OM，∵△GDH和△MHN都是等腰直角三角形，∴DH＝HG，HN＝MN
在R t △OGH中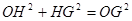，，設(shè)DH＝x，則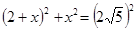
解得x＝2 或x＝－4（舍去）
在R t △OMN中，，設(shè)HN＝y，
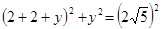∴，解得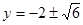（舍去負值）
∴
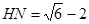
考點：圓的弧度和勾股定理
點評：該題看似復雜，其實所用知識點都是很常見的，求弧的度數(shù)主要是看該弧所對圓心角的度數(shù)，直角三角形中的邊長應多考慮用勾股定理。