
【題目】如圖,在平面直角坐標系中,△ABC的三個頂點坐標為A(1,-4) ,B(3,-3) ,C(1,-1).(每個小方格都是邊長為一個單位長度的正方形)
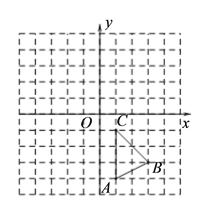
(1)將△ABC沿y軸方向向上平移5個單位,畫出平移后得到的△A1B1C1;
(2)將△ABC繞點O順時針旋轉90°,畫出旋轉后得到的△A2B2C2,并直接寫出點A旋轉到點A2所經過的路徑長.
【答案】(1)畫圖見解析;(2)畫圖見解析,點A旋轉到點A2所經過的路徑長為![]()
【解析】
(1)按題中要求在平面直角坐標系中畫出點A1、B1、C1三點,再順次連接這三點即可得到所求三角形;
(2)連接OA,在第三象限作OA2⊥OA,并使OA2=OA,即可得到點A2,同法作出點B2、C2,再順次連接所得三點即可得到所求三角形;由題意和所在圖形可知,點A旋轉到A2所經過路徑的長度是以點O為圓心,OA為半徑,圓心角度數為90度的弧的長度,因此根據題中已知條件計算出![]() 的長度即可;
的長度即可;
(1)如下圖,△A1B1C1為所求三角形:
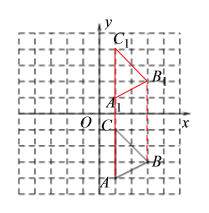
(2)如下圖,△A2B2C2為所求三角形:
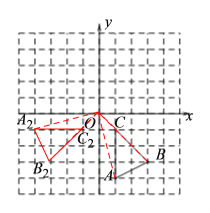
如上圖,由題意可知點A旋轉到點A2所經過的路徑是![]() ,
,
∵OA=![]() ,∠AOA2=90°,
,∠AOA2=90°,
∴![]() .
.
∴點A旋轉到點A2所經過的路徑長為:![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,EF∥AD,∠1=∠2,∠BAC=70°.將求∠AGD的過程填寫完整.
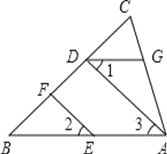
∵EF∥AD,(________)
∴∠2=______.(兩直線平行,同位角相等;)
又∵∠1=∠2,(________)
∴∠1=∠3.(________)
∴AB∥DG.(________)
∴∠BAC+______=180°(________)
又∵∠BAC=70°,(________)
∴∠AGD=______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一個關于數學的故事,蓬蓬國王為了獲得貧窮老百的支持,圖一個“樂善好施”的好名聲,決定施舍每個男人1美元,每個女人0.4美元.為了不使自己花費過多,他想來想去,最后想出了一個方法,決定在正午12時去一個貧困的山村.他十分清楚,在那時,村莊里有60%的男人都外出打獵去了,外出打獵的都不用給錢.已知該村莊里共有1200人,請問:
(1)若該村莊男人共有400人,則國王會用去多少美元?
(2)若該村莊女人共有400人,則國王會用去多少美元?
(3)有人說國王用去的錢數與村莊里男人和女人的具體數目無關,你認為正確嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若兩個有理數的和等于這兩個有理數的積,則稱這兩個有理數互為相依數.例如:有理數![]() 與3,因為
與3,因為![]() +3=
+3=![]() ×3.所以有理數與
×3.所以有理數與![]() 與3是互為相依數.
與3是互為相依數.
(1)直接判斷下列兩組有理數是否互為相依數,
①-5與-2;②-3與![]() ;
;
(2)若有理數![]() 與-7 互為相依數,求m的值;
與-7 互為相依數,求m的值;
(3)若有理數a與b互為相依數,b與c互為相反數,求式子5(ab+![]() c)-2(
c)-2(![]() a-b)-4的值;
a-b)-4的值;
(4)對于有理數a(a≠0,1),對它進行如下操作:取a的相依數,得到a1;取a1的倒數,得到a2;取a2的相依數,得到a3;取a3的倒數,得到a4;…,;依次按如上的操作得到一組數a1,a2,a3,…,an , 若a=![]() ,試著直接寫出a1,a2,a3,…, a2018的和.
,試著直接寫出a1,a2,a3,…, a2018的和.
查看答案和解析>>
科目:初中數學 來源: 題型:
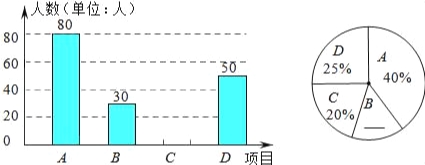
【題目】某中學開展“陽光體育一小時”活動,根據學校實際情況,決定開設A:踢毽子;B:籃球;C:跳繩;D:乒乓球四種運動項目.為了解學生最喜歡哪一種運動項目,隨機抽取了一部分學生進行調查,并將調查結果繪制成如下兩個統計圖.
請結合圖中的信息解答下列問題:
(1)本次共調查了多少名學生?
(2)請將兩個統計圖補充完整;
(3)請求出C項目所占的圓心角是 72 度;
(4)若該中學有1200名學生,喜歡籃球運動項目的學生約有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形![]() 是正方形,
是正方形,![]() 是直線
是直線![]() 上任意一點,
上任意一點,![]() 于點
于點![]() ,
,![]() 于點
于點![]() .當點G在BC邊上時(如圖1),易證DF-BE=EF.
.當點G在BC邊上時(如圖1),易證DF-BE=EF.

(1)當點![]() 在
在![]() 延長線上時,在圖2中補全圖形,寫出
延長線上時,在圖2中補全圖形,寫出![]() 、
、![]() 、
、![]() 的數量關系,并證明;
的數量關系,并證明;
(2)當點![]() 在
在![]() 延長線上時,在圖3中補全圖形,寫出
延長線上時,在圖3中補全圖形,寫出![]() 、
、![]() 、
、![]() 的數量關系,不用證明.
的數量關系,不用證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,E為AB邊上一點,DE=DC,點F為線段DE上一點,滿足∠DFC=∠A,連結CE.
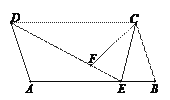
(1)求證:AD=FC;
(2)求證:CE是∠BCF的角平分線.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com