
【題目】如圖,在△ABC中,∠C=90°,AC=BC= ![]() ,將△ABC繞點A順時針方向旋轉60°到△AB′C′的位置,連接C′B,則C′B= .
,將△ABC繞點A順時針方向旋轉60°到△AB′C′的位置,連接C′B,則C′B= . 
【答案】![]()
【解析】解:如圖,連接BB′,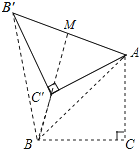
∵△ABC繞點A順時針方向旋轉60°得到△AB′C′,
∴AB=AB′,∠BAB′=60°,
∴△ABB′是等邊三角形,
∴AB=BB′,
在△ABC′和△B′BC′中,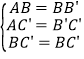 ,
,
∴△ABC′≌△B′BC′(SSS),
∴∠ABC′=∠B′BC′,
延長BC′交AB′于D,
則BD⊥AB′,
∵∠C=90°,AC=BC= ![]() ,
,
∴AB= ![]() =2,
=2,
∴BD=2× ![]() =
= ![]() ,C′D=
,C′D= ![]() ×2=1,∴BC′=BD﹣C′D=
×2=1,∴BC′=BD﹣C′D= ![]() ﹣1.所以答案是:
﹣1.所以答案是: ![]() ﹣1.
﹣1.
【考點精析】認真審題,首先需要了解旋轉的性質(①旋轉后對應的線段長短不變,旋轉角度大小不變;②旋轉后對應的點到旋轉到旋轉中心的距離不變;③旋轉后物體或圖形不變,只是位置變了).


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:初中數學 來源: 題型:
【題目】一個不透明的布袋里裝有4個大小,質地都相同的乒乓球,球面上分別標有數字1,﹣2,3,﹣4,小明先從布袋中隨機摸出一個球(不放回去),再從剩下的3個球中隨機摸出第二個乒乓球.
(1)共有種可能的結果.
(2)請用畫樹狀圖或列表的方法求兩次摸出的乒乓球的數字之積為偶數的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,△ABC中,D是BC邊上一點,E是AD的中點,過點A作BC的平行線交CE的延長線于F,且AF=BD,連接BF.
(1)求證:D是BC的中點;
(2)若AB=AC,試判斷四邊形AFBD的形狀,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,已知AD>AB.
(1)實踐與操作:作∠BAD的平分線交BC于點E,在AD上截取AF=AB,連接EF;(要求:尺規作圖,保留作圖痕跡,不寫作法)
(2)猜想并證明:猜想四邊形ABEF的形狀,并給予證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把△EFP放置在菱形ABCD中,使得頂點E,F,P分別在線段AB,AD,AC上,已知EP=FP=6,EF=6 ![]() ,∠BAD=60°,且AB>6
,∠BAD=60°,且AB>6 ![]() .
.
(1)求∠EPF的大小;
(2)若AP=10,求AE+AF的值;
(3)若△EFP的三個頂點E、F、P分別在線段AB、AD、AC上運動,請直接寫出AP長的最大值和最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=﹣x+5與雙曲線y= ![]() (x>0)相交于A,B兩點,與x軸相交于C點,△BOC的面積是
(x>0)相交于A,B兩點,與x軸相交于C點,△BOC的面積是 ![]() .若將直線y=﹣x+5向下平移1個單位,則所得直線與雙曲線y=
.若將直線y=﹣x+5向下平移1個單位,則所得直線與雙曲線y= ![]() (x>0)的交點有( )
(x>0)的交點有( )
A.0個
B.1個
C.2個
D.0個,或1個,或2個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,邊長為1的正方形OA1B1C1的兩邊在坐標軸上,以它的對角線OB1為邊作正方形OB1B2C2 , 再以正方形OB1B2C2的對角線OB2為邊作正方形OB2B3C3 , 以此類推…、則正方形OB2015B2016C2016的頂點B2016的坐標是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解學生家長對孩子用手機的態度問題,隨機抽取了100名家長進行問卷調查,每位學生家長只有一份問卷,且每份問卷僅表明一種態度(這100名家長的問卷真實有效),將這100份問卷進行回收整理后,繪制了如下兩幅不完整的統計圖.
(1)“從來不管”的問卷有份,在扇形圖中“嚴加干涉”的問卷對應的圓心角為 .
(2)請把條形圖補充完整.
(3)若該校共有學生2000名,請估計該校對手機問題“嚴加干涉”的家長有多少人.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com