【題目】端午節當天，小明帶了四個粽子（除味道不同外，其它均相同），其中兩個是大棗味的，另外兩個是火腿味的，準備按數量平均分給小紅和小剛兩個好朋友．
（1）請你用樹狀圖或列表的方法表示小紅拿到的兩個粽子的所有可能性．
（2）請你計算小紅拿到的兩個粽子剛好是同一味道的概率．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】如圖，在Rt△AOB中，直角邊OA、OB分別在x軸的負半軸和y軸的正半軸上，將△AOB繞點B逆時針旋轉90°后，得到△A′O′B，且反比例函數y= 
的圖象恰好經過斜邊A′B的中點C，若SABO=4，tan∠BAO=2，則k= ．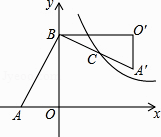 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在矩形ABCD中，連接對角線AC、BD，將△ABC沿BC方向平移，使點B移到點C，得到△DCE． 
（1）求證：△ACD≌△EDC；
（2）請探究△BDE的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，△ABC位于第二象限，點A的坐標是（﹣2，3），先把△ABC向右平移4個單位長度得到△A1B1C1 ， 再作與△A1B1C1關于x軸對稱的△A2B2C2 ， 則點A的對應點A2的坐標是（ ）
A.（﹣3，2）
B.（2，﹣3）
C.（1，﹣2）
D.（﹣1，2）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】拋物線y=ax2+bx+3經過點A（1，0）和點B（5，0）．
（1）求該拋物線所對應的函數解析式；
（2）該拋物線與直線y= 
x+3相交于C、D兩點，點P是拋物線上的動點且位于x軸下方，直線PM∥y軸，分別與x軸和直線CD交于點M、N．
①連結PC、PD，如圖1，在點P運動過程中，△PCD的面積是否存在最大值？若存在，求出這個最大值；若不存在，說明理由；
②連結PB，過點C作CQ⊥PM，垂足為點Q，如圖2，是否存在點P，使得△CNQ與△PBM相似？若存在，求出滿足條件的點P的坐標；若不存在，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下面的統計圖反映了我國與“一帶一路”沿線部分地區的貿易情況． 2011﹣2016年我國與東南亞地區和東歐地區的貿易額統計圖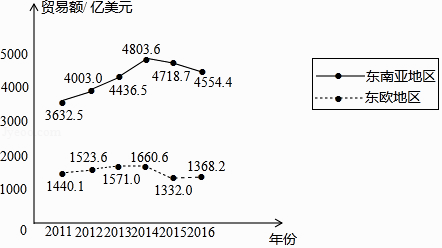
（以上數據摘自《“一帶一路”貿易合作大數據報告（2017）》）
根據統計圖提供的信息，下列推理不合理的是（ ）
A.與2015年相比，2016年我國與東歐地區的貿易額有所增長
B.2011﹣2016年，我國與東南亞地區的貿易額逐年增長
C.2011﹣2016年，我國與東南亞地區的貿易額的平均值超過4200億美元
D.2016年我國與東南亞地區的貿易額比我國與東歐地區的貿易額的3倍還多
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，函數y= 
（x＞0）的圖象與直線y=x﹣2交于點A（3，m）． 
（1）求k、m的值；
（2）已知點P（n，n）（n＞0），過點P作平行于x軸的直線，交直線y=x﹣2于點M，過點P作平行于y軸的直線，交函數y= （x＞0）的圖象于點N． ①當n=1時，判斷線段PM與PN的數量關系，并說明理由；
②若PN≥PM，結合函數的圖象，直接寫出n的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，多邊形的各頂點都在方格紙的格點（橫豎格子線的交錯點）上，這樣的多邊形稱為格點多邊形，它的面積S可用公式S=a+ 
b﹣1（a是多邊形內的格點數，b是多邊形邊界上的格點數）計算，這個公式稱為“皮克定理”．現用一張方格紙共有200個格點，畫有一個格點多邊形，它的面積S=40．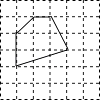
（1）這個格點多邊形邊界上的格點數b=（用含a的代數式表示）．
（2）設該格點多邊形外的格點數為c，則c﹣a= ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在梯形ABCD中，AD∥BC，點E在邊AD上，CE與BD相交于點F，AD=4，AB=5，BC=BD=6，DE=3．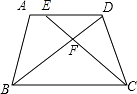 
（1）求證：△DFE∽△DAB；
（2）求線段CF的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
