
【題目】閱讀下列材料:一般地,![]() 個相同的因數
個相同的因數![]() 相乘
相乘 ![]() ,記為
,記為![]() .如
.如![]() ,此時,
,此時,![]() 叫做以
叫做以![]() 為底
為底![]() 的對數,記為
的對數,記為![]() (即
(即![]() ).一般地,若
).一般地,若![]() ,(
,(![]() 且
且![]() ,
,![]() ),則
),則![]() 叫做以
叫做以![]() 為底
為底![]() 的對數,記為
的對數,記為![]() (即
(即![]() ).如
).如![]() ,則
,則![]() 叫做以
叫做以![]() 為底
為底![]() 的對數,記為
的對數,記為![]() (即
(即![]() ).
).
(1)計算以下各對數的值:![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(2)觀察(1)中三數![]() 、
、![]() ,
,![]() 之間滿足怎樣的關系式,
之間滿足怎樣的關系式,![]() 、
、![]() 、
、![]() 之間又滿足怎樣的關系式;
之間又滿足怎樣的關系式;
(3)由(2)的結果,你能歸納出一個一般性的結論嗎?![]() __________.(
__________.(![]() 且
且![]() ,
,![]() ,
,![]() )
)
(4)根據冪的運算法則:![]() 以及對數的含義證明上述結論.
以及對數的含義證明上述結論.
【答案】(1)2,4,6;(2)log24+log216=log264;(3)logaM+logaN=loga(MN);(4)證明見解析.
【解析】
(1)根據對數的定義求解;
(2)認真觀察,不難找到規律:4×16=64,log24+log216=log264;
(3)有特殊到一般,得出結論:logaM+logaN=loga(MN);
(4)首先可設logaM=b1,logaN=b2,再根據冪的運算法則:anam=an+m以及對數的含義證明結論.
(1)∵22=4,∴log24=2,
∵24=16,∴log216=4,
∵26=64,∴log264=6;
(2)4×16=64,log24+log216=log264;
(3)logaM+logaN=loga(MN);
(4)證明:設logaM=x,logaN=y,
則ax=M,ay=N,
∴MN=axay=ax+y,
∴x+y=loga(MN)即logaM+logaN=loga(MN).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子里裝有只有顏色不同的黑、白兩種球共50個,小穎做摸球實驗,她將盒子里面的球攪勻后從中隨機摸出一個球記下顏色,再把它放回盒子中,不斷重復上述過程,下表是試驗中的一組統計數據:
摸到球的次數 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次數 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的概率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)請估計當![]() 很大時,摸到白球的頻率將會接近______;(精確到0.1);
很大時,摸到白球的頻率將會接近______;(精確到0.1);
(2)假如隨機摸一次,摸到白球的概率P(白球)=______;
(3)試估算盒子里白色的球有多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在4×4的正方形(每個小正方形的邊長均為1)網格中,以A為頂點,其他三個頂點都在格點(網格的交點)上,且面積為2的平行四邊形共有多少個?( )

A.12B.16C.24D.25
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有下列說法:(![]() )單項式
)單項式![]() 的系數、次數都是
的系數、次數都是![]() ;(
;(![]() )多項式
)多項式![]() 的系數是
的系數是![]() ,它是三次二項式;(
,它是三次二項式;(![]() )單項式
)單項式![]() 與
與![]() 都是七次單項式;(4)單項式
都是七次單項式;(4)單項式![]() 和
和![]() 的系數分別是
的系數分別是![]() 或
或![]() ;(
;(![]() )
)![]() 是二次單項式;(
是二次單項式;(![]() )
)![]() 與
與![]() 都是整式,其中正確的說法有( ).
都是整式,其中正確的說法有( ).
A.![]() 個B. C.
個B. C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,以點C(1,1)為圓心,2為半徑作圓,交x軸于A,B兩點,點P在優弧![]() 上.
上.
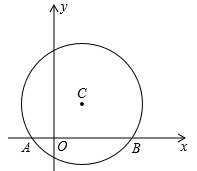
(1)求出A,B兩點的坐標;
(2)試確定經過A、B且以點P為頂點的拋物線解析式;
(3)在該拋物線上是否存在一點D,使線段OP與CD互相平分?若存在,求出點D的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在銳角△ABC中,AB=5,tanC=3,BD⊥AC于點D,BD=3,點P從點A出發,以每秒1個單位長度的速度沿AB向終點B運動,過點P作PE∥AC交邊BC于點E,以PE為邊作Rt△PEF,使∠EPF=90°,點F在點P的下方,且EF∥AB.設△PEF與△ABD重疊部分圖形的面積為S(平方單位)(S>0),點P的運動時間為t(秒)(t>0).
(1)求線段AC的長.
(2)當△PEF與△ABD重疊部分圖形為四邊形時,求S與t之間的函數關系式.
(3)若邊EF與邊AC交于點Q,連結PQ,如圖②.
①當PQ將△PEF的面積分成1:2兩部分時,求AP的長.
②直接寫出PQ的垂直平分線經過△ABC的頂點時t的值.
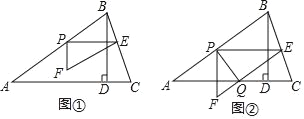
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,Rt△ABC的三個頂點分別是A(-3,2),B(0,4),C(0,2).
(1)將△ABC以點C為旋轉中心旋轉180°,畫出旋轉后對應的△A1B1C;平移△ABC,若點A的對應點A2的坐標為(0,-4),畫出平移后對應的△A2B2C2;
(2)若將△A1B1C繞某一點旋轉可以得到△A2B2C2,請直接寫出旋轉中心的坐標;
(3)在x軸上有一點P,使得PA+PB的值最小,請直接寫出點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,過點A作⊙O的切線,交OC的延長線于點D,∠D=30°
(1)求∠B的度數;
(2)若OD⊥AB,BC=5,求AD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
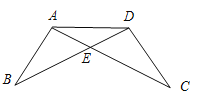
【題目】在一次數學課上,王老師在黑板上畫出一幅圖,并寫下了四個等式:
①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
(1)上述四個條件中,由哪兩個條件可以判定![]() 是等腰三角形?用序號寫出所有成立的情形.
是等腰三角形?用序號寫出所有成立的情形.
(2)請選擇(1)中的一種情形,寫出證明過程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com