
(8分)一位同學拿了兩塊相同的 三角尺
三角尺 和
和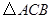 做了一個探究活動:將
做了一個探究活動:將 的直角頂點
的直角頂點 放在
放在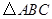 的斜邊
的斜邊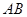 的中點處,設
的中點處,設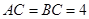 .
.
(1)如圖(1),兩三角尺的重疊部分為 ,則重疊部分的面積為 ,周長為 .
,則重疊部分的面積為 ,周長為 .
(2)將圖(1)中的 繞頂點
繞頂點 逆時針旋轉
逆時針旋轉 ,得到圖(2),此時重疊部分的面積為 ,周長為 .
,得到圖(2),此時重疊部分的面積為 ,周長為 .
(3)如果將 繞
繞 旋轉到不同于圖(1)和圖(2)的圖形,如圖(3),請你猜想此時重疊部分的面積為 .
旋轉到不同于圖(1)和圖(2)的圖形,如圖(3),請你猜想此時重疊部分的面積為 .
(4)在圖(3)情況下,若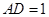 ,求出重疊部分圖形的周長.
,求出重疊部分圖形的周長.
(1)4,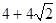 (2)4,8(3)4(4)
(2)4,8(3)4(4)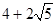
解析試題分析:解答:連結CM
證明△ADM≌△CGM
(∠AMD=∠CMG,∠MAD=∠MCG=45°,AM=CM)-----------------------6分
于是AD="CG" ,DM="GM"
所求周長L=CD+DM+MG+GC=AD+CD+2DM=4+2DM。
取AC的中點E,連接ME ,即ME為△ABC的中位線, ME="2" ,又因為E為AC中點所以AE=2。因為AD="1" 所以DE="2-1=1" 利用勾股定理在Rt△DME中得到DM=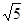 ,所以周長為4+2
,所以周長為4+2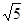 --------------------------------------------------8分
--------------------------------------------------8分
考點:本題考查了勾股定理的應運算
點評:此類試題屬于難度一般的試題,考生在解答時務必對周長和面積等基本求解方法熟練掌握


 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案科目:初中數學 來源:2012-2013學年云南省九年級11月月考數學試卷(解析版) 題型:解答題
(8分)一位同學拿了兩塊相同的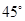 三角尺
三角尺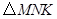 和
和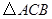 做了一個探究活動:將
做了一個探究活動:將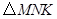 的直角頂點
的直角頂點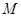 放在
放在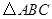 的斜邊
的斜邊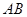 的中點處,設
的中點處,設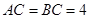 .
.

(1)如圖(1),兩三角尺的重疊部分為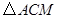 ,則重疊部分的面積為 ,周長為 .
,則重疊部分的面積為 ,周長為 .
(2)將圖(1)中的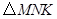 繞頂點
繞頂點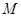 逆時針旋轉
逆時針旋轉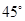 ,得到圖(2),此時重疊部分的面積為 ,周長為 .
,得到圖(2),此時重疊部分的面積為 ,周長為 .
(3)如果將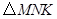 繞
繞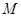 旋轉到不同于圖(1)和圖(2)的圖形,如圖(3),請你猜想此時重疊部分的面積為 .
旋轉到不同于圖(1)和圖(2)的圖形,如圖(3),請你猜想此時重疊部分的面積為 .
(4)在圖(3)情況下,若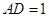 ,求出重疊部分圖形的周長.
,求出重疊部分圖形的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com