【題目】小亮早晨從家騎車到學校，先上坡后下坡，所行路程y（米）與時間x（分鐘）的關系如圖所示，若返回時上坡、下坡的速度仍與去時上、下坡的速度分別相同，則小明從學校騎車回家用的時間是分鐘．
【答案】63 
【解析】解：由圖可得，去校時，上坡路的距離為2000米，所用時間為18分，
∴上坡速度=2000÷18= 
米/分，
下坡路的距離是9000﹣2000=7000米，所用時間為20﹣18=2分，
∴下坡速度=7000÷2=3500米/分；
∵去學校時的上坡回家時變為下坡、去學校時的下坡回家時變為上坡，
∴小明從學校騎車回家用的時間是：7000÷ +2000÷3500=63+ =63 分鐘．
所以答案是：63 ．
【考點精析】通過靈活運用函數的圖象，掌握函數的圖像是由直角坐標系中的一系列點組成；圖像上每一點坐標（x，y）代表了函數的一對對應值，他的橫坐標x表示自變量的某個值，縱坐標y表示與它對應的函數值即可以解答此題．
科學實驗活動冊系列答案科目：初中數學 來源： 題型：
【題目】完成下面推理過程．在括號內的橫線上填空或填上推理依據．
如圖，已知：AB∥EF，EP⊥EQ，∠EQC+∠APE=90°，求證：AB∥CD
證明：∵AB∥EF
∴∠APE=（）
∵EP⊥EQ
∴∠PEQ=（）
即∠QEF+∠PEF=90°
∴∠APE+∠QEF=90°
∵∠EQC+∠APE=90°
∴∠EQC=
∴EF∥（）
∴AB∥CD（）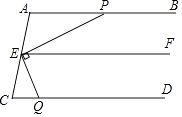
查看答案和解析>>
科目：初中數學 來源： 題型：
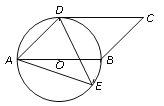
【題目】如圖，四邊形ABCD是平行四邊形，以AB為直徑的⊙O經過點D，E是⊙O上一點，且∠AED=45．
(1)試判斷CD與⊙O的位置關系，并證明你的結論；
(2)若⊙O的半徑為3，sin∠ADE=
，求AE的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數y=﹣x+5的圖象與反比例函數y=kx-1（k≠0）在第一象限的圖象交于A（1，n）和B兩點．
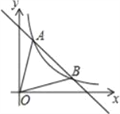
（1）求反比例函數的解析式與點B坐標；
（2）求△AOB的面積；
（3）在第一象限內，當一次函數y=﹣x+5的值小于反比例函數y=kx-1（k≠0）的值時，寫出自變量x的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
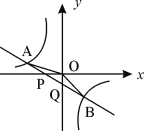
【題目】 （2016湖北鄂州第14題）如圖，已知直線 
與x軸、y軸相交于P、Q兩點，與y=
的圖像相交于A（－2，m）、B（1，n）兩點，連接OA、OB. 給出下列結論： ①k1k2<0；②m+
n=0； ③S△AOP= S△BOQ；④不等式k1x+b＞的解集是x<－2或0<x<1，其中正確的結論的序號是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
