
【題目】在平面直角坐標系中,邊長為3的正方形OABC的兩頂點A、C分別在y軸、x軸的正半軸上,點O在原點。現將正方形OABC繞O點順時針旋轉,當A點第一次落在直線y=x上時停止旋轉,旋轉過程中,AB邊交直線y=x于點M,BC邊交x軸于點N(如圖).在旋轉正方形OABC的過程中,△MBN的周長為________
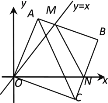
【答案】4.
【解析】
利用全等把△MBN的各邊整理到成與正方形的邊長有關的式子即可.
解:如圖所示:延長BA交y軸于E點,
則∠AOE=45°-∠AOM,∠CON=90°-45°-∠AOM=45°-∠AOM,
∴∠AOE=∠CON.
又∵OA=OC,∠OAE=180°-90°=90°=∠OCN,
在△OAE和△OCN中,
∠EOA=∠CON,OA=OC,∠OAE=∠OCN,
,
∴△OAE≌△OCN(ASA).
∴OE=ON,AE=CN.
在△OME和△OMN中,
OE=OC,∠EOM=∠COM,OM=OM,
∴△OME≌△OMN(SAS).
∴MN=ME=AM+AE.
∴MN=AM+CN,
∴△MBN的周長=MN+BN+BM=AM+CN+BN+BM=AB+BC=6.
“點睛”此題主要考查了旋轉的性質以及全等三角形的判定與性質等知識,注意求一些線段的長度或角的度數,總要整理到已知線段的長度上或已知角的度數上進而得出是解題關鍵.


科目:初中數學 來源: 題型:
【題目】閱讀材料并完成任務.

萊昂哈德·歐拉是18世紀數學界最杰出的人物之一,瑞士著名的數學家、物理學家,他不但為數學界作出貢獻,更把整個數學推至物理的領域;同時,也是數學史上研究成果最多的數學家,平均每年寫出八百多頁的論文,還寫了大量的力學、分析學、幾何學等的課本,《無窮小分析引論》《微分學原理》《積分學原理》等都成為數學界中的經典著作.因此,被稱為歷史上最偉大的兩位數學家之一(另一位是卡爾·弗里德里克·高斯).在數學成就上,歐拉最先把關于![]() 的多項式用記號
的多項式用記號![]() 的形式來表示(
的形式來表示(![]() 可用其他字母代替,但不同的字母表示不同的多項式),例如
可用其他字母代替,但不同的字母表示不同的多項式),例如![]() ,當
,當![]() 時,多項式的值用
時,多項式的值用![]() 來表示,即
來表示,即![]() ;當
;當![]() 時,多項式的值用
時,多項式的值用![]() 來表示,記為
來表示,記為![]() .
.
任務:
已知![]() ;
;![]() .
.
請你根據材料中代入求值的方法解決下列問題:
(1)求![]() 的值;
的值;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
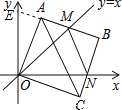
【題目】如圖1,在平面直角坐標系中,直線AB分別交x軸、y軸于點![]() 點
點![]() 且a、b滿足
且a、b滿足![]() .
.
![]() ______;
______;![]() ______.
______.
![]() 點P在直線AB的右側,且
點P在直線AB的右側,且![]() ,
,
![]() 若點P在x軸上,則點P的坐標為______;
若點P在x軸上,則點P的坐標為______;
![]() 若
若![]() 為直角三角形,求點P的坐標;
為直角三角形,求點P的坐標;
![]() 如圖2,在
如圖2,在![]() 的條件下,
的條件下,![]() 且點P在第四象限,AP與y軸交于點M,BP與x軸交于點N,連接
且點P在第四象限,AP與y軸交于點M,BP與x軸交于點N,連接![]() 求證:
求證:![]() 提示:過點P作
提示:過點P作![]() 交x軸于
交x軸于![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,對角線AC,BD相交于點O,過點D作對角線BD的垂線交BA的延長線于點E.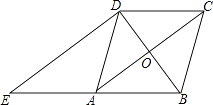
(1)證明:四邊形ACDE是平行四邊形;
(2)若AC=8,BD=6,求△ADE的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,AB為⊙O的直徑,PD切⊙O于點C,與BA的延長線交于點D,DE⊥PO交PO延長線于點E,連接PB,∠EDB=∠EPB.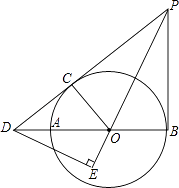
(1)求證:PB是⊙O的切線;
(2)若PB=9,DB=12,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x,y的方程組![]()
(1)請直接寫出方程![]() 的所有正整數解
的所有正整數解
(2)若方程組的解滿足x+y=0,求m的值
(3)無論實數m取何值,方程x-2y+mx+5=0總有一個固定的解,請直接寫出這個解?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖①是一個長為 a,寬為 b 的長方形.現將相等的長方形若干,拼接組成如下圖 形.
(1)將圖①中所得的四塊長為 a,寬為 b 的小長方形拼成一個正方形(如圖②).請利用 圖②中陰影部分面積的不同表示方法,直接寫出代數式(a+b)2、(a﹣b)2、ab 之間的等量關系是 ;
(2)根據(2)題中的等量關系,解決如下問題:已知 m+n=6,mn=5,則 m﹣n= ;
(3)將圖①中的長方形和圖③中的兩個邊長分別為 a、b 的正方形若干個,拼成如圖④的長方形,則圖④中的長方形的面積可以用兩種不同的方法表示,則關系式 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2﹣4![]() x+12+m=0.
x+12+m=0.
(1)若方程的一個根是![]() ,求m的值及方程的另一根;
,求m的值及方程的另一根;
(2)若方程的兩根恰為等腰三角形的兩腰,而這個三角形的底邊為m,求m的值及這個等腰三角形的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com