
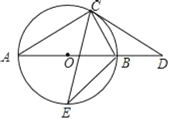
【題目】AB為⊙O直徑,C為⊙O上的一點,過點C的切線與AB的延長線相交于點D,CA=CD.
(1)連接BC,求證:BC=OB;
(2)E是![]() 中點,連接CE,BE,若BE=2,求CE的長.
中點,連接CE,BE,若BE=2,求CE的長.
【答案】(1)見解析;(2)1+![]() .
.
【解析】
(1)連接OC,根據圓周角定理、切線的性質得到∠ACO=∠DCB,根據CA=CD得到∠CAD=∠D,證明∠COB=∠CBO,根據等角對等邊證明;
(2)連接AE,過點B作BF⊥CE于點F,根據勾股定理計算即可.
(1)證明:連接OC,
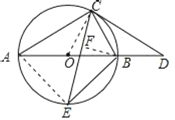
∵AB為⊙O直徑,
∴∠ACB=90°,
∵CD為⊙O切線
∴∠OCD=90°,
∴∠ACO=∠DCB=90°﹣∠OCB,
∵CA=CD,
∴∠CAD=∠D.
∴∠COB=∠CBO.
∴OC=BC.
∴OB=BC;
(2)連接AE,過點B作BF⊥CE于點F,
∵E是AB中點,
∴![]() ,
,
∴AE=BE=2.
∵AB為⊙O直徑,
∴∠AEB=90°.
∴∠ECB=∠BAE=45°,![]() ,
,
∴![]() .
.
∴CF=BF=1.
∴![]() .
.
∴![]() .
.


科目:初中數學 來源: 題型:
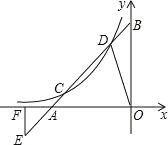
【題目】已知直線y=x+3與x軸、y軸分別交于A,B點,與y=![]() (x<0)的圖象交于C、D點,E是點C關于點A的中心對稱點,EF⊥OA于F,若△AOD的面積與△AEF的面積之和為
(x<0)的圖象交于C、D點,E是點C關于點A的中心對稱點,EF⊥OA于F,若△AOD的面積與△AEF的面積之和為![]() 時,則k=_____.
時,則k=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小林在沒有量角器和圓規的情況下,利用刻度尺和一副三角板畫出了一個角的平分線,他的作法是這樣的:如圖:
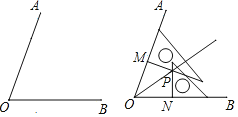
(1)利用刻度尺在∠AOB的兩邊OA,OB上分別取OM=ON;
(2)利用兩個三角板,分別過點M,N畫OM,ON的垂線,交點為P;
(3)畫射線OP.
則射線OP為∠AOB的平分線.請寫出小林的畫法的依據______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
厲害了,我的國!
近年來,中國對外開放的步伐加快,與世界經濟的融合度日益提高,中國經濟穩定增長是世界經濟復蘇的主要動力.“十二五”時期,按照2010年美元不變價計算,中國對世界經濟增長的年均貢獻率達到30.5%,躍居全球第一,與“十五”和“十一五”時期14.2%的年均貢獻率相比,提高16.3個百分點,同期美國和歐元區分別為17.8%和4.4%.分年度來看,2011、2012、2013、2014、2015年,中國對世界經濟增長的貢獻率分別為28.6%、31.7%、32.5%、29.7%、30.0%,而美國分別為11.8%、20.4%、15.2%、19.6%、21.9%.
2016年,中國對世界經濟增長的貢獻率仍居首位,預計全年經濟增速為6.7%左右,而世界銀行預測全球經濟增速為2.4%左右.按2010年美元不變價計算,2016年中國對世界經濟增長的貢獻率仍然達到33.2%.如果按照2015年價格計算,則中國對世界經濟增長的貢獻率會更高一點,根據有關國際組織預測,2016年中國、美國、日本經濟增速分別為6.7%、1.6%、0.6%.
根據以上材料解答下列問題:
(1)選擇合適的統計圖或統計表將2013年至2015年中國和美國對世界經濟增長的貢獻率表示出來;
(2)根據題中相關信息,2016年中國經濟增速大約是全球經濟增速的 倍(保留1位小數);
(3)根據題中相關信息,預估2017年中國對世界經濟增長的貢獻率約為 ,你的預估理由是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2+2(m﹣1)x+m2﹣3=0有兩個不相等的實數根.
(1)求m的取值范圍;
(2)若m為非負整數,且該方程的根都是無理數,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明騎自行車上學,開始以正常速度勻速行駛,但行至中途時,自行車出了故障,只好停下來修車,車修好后,因怕耽誤上課,他比修車前加快了速度繼續勻速行駛,下面是行駛路程s(m)關于時間t(min)的函數圖象,那么符合小明行駛情況的大致圖象是()
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為積極響應市委政府“加快建設天藍水碧地綠的美麗長沙”的號召,我市某街道決定從備選的五種樹中選購一種進行栽種.為了更好地了解社情民意,工作人員在街道轄區范圍內隨機抽取了部分居民,進行“我最喜歡的一種樹”的調查活動(每人限選其中一種樹),并將調查結果整理后,繪制成如圖兩個不完整的統計圖:

請根據所給信息解答以下問題:
(1)這次參與調查的居民人數為: ;
(2)請將條形統計圖補充完整;
(3)請計算扇形統計圖中“楓樹”所在扇形的圓心角度數;
(4)已知該街道轄區內現有居民8萬人,請你估計這8萬人中最喜歡玉蘭樹的有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
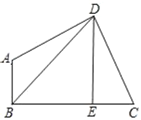
【題目】已知:如圖,在四邊形ABCD中,∠ABC=∠ADC=90°,DE⊥BC于E,連接BD,設AD=m,DC=n,BE=p,DE=q.
(1)若tanC=2,BE=3,CE=2,求點B到CD的距離;
(2)若m=n, BD=3![]() ,求四邊形ABCD的面積.
,求四邊形ABCD的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com