
【題目】如圖1,直線y=x+1與拋物線y=2x2相交于A、B兩點,與y軸交于點M,M、N關于x軸對稱,連接AN、BN.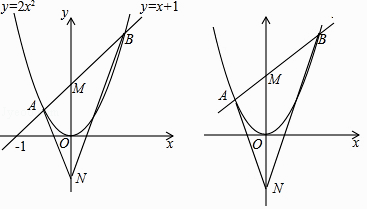
(1)①求A、B的坐標;②求證:∠ANM=∠BNM;
(2)如圖2,將題中直線y=x+1變為y=kx+b(b>0),拋物線y=2x2變為y=ax2(a>0),其他條件不變,那么∠ANM=∠BNM是否仍然成立?請說明理由.
【答案】
(1)
解:①由已知得2x2=x+1,解得 ![]() 或x=1,
或x=1,
當 ![]() 時,
時, ![]() ,當x=1時,y=2,
,當x=1時,y=2,
∴A、B兩點的坐標分別為( ![]() ,
, ![]() ),( 1,2);
),( 1,2);
②如圖1,過A作AC⊥y軸于C,過B作BD⊥y軸于D,
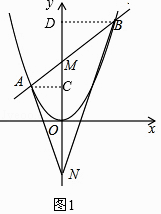
由①及已知有A( ![]() ,
, ![]() ),B( 1,2),且OM=ON=1,
),B( 1,2),且OM=ON=1,
∴ 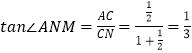 ,
, ![]() ,
,
∴tan∠ANM=tan∠BNM,
∴∠ANM=∠BNM;
(2)
解:∠ANM=∠BNM成立,
①當k=0,△ABN是關于y軸的軸對稱圖形,
∴∠ANM=∠BNM;
②當k≠0,根據題意得:OM=ON=b,設 ![]() 、B
、B ![]() .
.
如圖2,過A作AE⊥y軸于E,過B作BF⊥y軸于F,
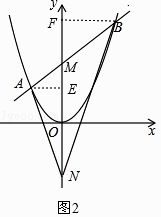
由題意可知:ax2=kx+b,即ax2﹣kx﹣b=0,
∴ ![]() ,
,
∵ ![]() =
= ![]() =
= ![]() =
= 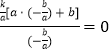 ,
,
∴ ![]() ,
,
∴Rt△AEN∽Rt△BFN,
∴∠ANM=∠BNM.
【解析】(1)①聯立直線和拋物線解析式可求得A、B兩點的坐標;②過A作AC⊥y軸于C,過B作BD⊥y軸于D,可分別求得∠ANM和∠BNM的正切值,可證得結論;(2)當k=0時,由對稱性可得出結論;當k≠0時,過A作AE⊥y軸于E,過B作BF⊥y軸于F,設 ![]() 、B
、B ![]() ,聯立直線和拋物線解析式,消去y,利用根與系數的關系,可求得
,聯立直線和拋物線解析式,消去y,利用根與系數的關系,可求得 ![]() ,則可證明Rt△AEN∽Rt△BFN,可得出結論.
,則可證明Rt△AEN∽Rt△BFN,可得出結論.
【考點精析】利用二次函數的性質對題目進行判斷即可得到答案,需要熟知增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,E是ABCD的邊CD的中點,延長AE交BC的延長線于點F.
(1)求證:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】夏季空調銷售供不應求,某空調廠接到一份緊急訂單,要求在10天內(含10天)完成任務,為提高生產效率,工廠加班加點,接到任務的第一天就生產了空調42臺,以后每天生產的空調都比前一天多2臺,由于機器損耗等原因,當日生產的空調數量達到50臺后,每多生產一臺,當天生產的所有空調,平均每臺成本就增加20元.
(1)設第x天生產空調y臺,直接寫出y與x之間的函數解析式,并寫出自變量x的取值范圍.
(2)若每臺空調的成本價(日生產量不超過50臺時)為2000元,訂購價格為每臺2920元,設第x天的利潤為W元,試求W與x之間的函數解析式,并求工廠哪一天獲得的利潤最大,最大利潤是多少.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是菱形,對角線AC與BD相交于O,AB=6cm, ∠BAO=30°,點F為AB的中點.
(1)求OF的長度;
(2)求AC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,二次函數y=ax2+bx+c(a≠0)的大致圖象如圖所示,則下列結論正確的是( ) 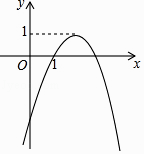
A.a<0,b<0,c>0
B.﹣ ![]() =1
=1
C.a+b+c<0
D.關于x的方程x2+bx+c=﹣1有兩個不相等的實數根
查看答案和解析>>
科目:初中數學 來源: 題型:
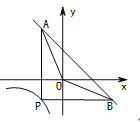
【題目】如圖,P為反比例函數![]() (x<0)在第三象限內圖象上的一點,過點P分別作x軸、y軸的垂線交一次函數y=-x+4的圖像于點A、B.若AO、BO分別平分∠BAP,∠ABP ,則k的值為___________.
(x<0)在第三象限內圖象上的一點,過點P分別作x軸、y軸的垂線交一次函數y=-x+4的圖像于點A、B.若AO、BO分別平分∠BAP,∠ABP ,則k的值為___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于實數p,q,我們用符號min{p,q}表示p,q兩數中較小的數,如min{1,2}=1,因此,min{﹣ ![]() ,﹣
,﹣ ![]() }=;若min{(x﹣1)2 , x2}=1,則x= .
}=;若min{(x﹣1)2 , x2}=1,則x= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com