
【題目】小波在復習時,遇到一個課本上的問題,溫故后進行了操作、推理與拓展.
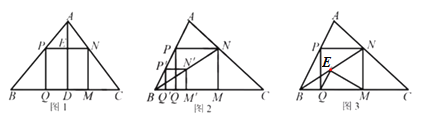
(1)溫故:如圖1,在△ABC中,AD⊥BC于點D,正方形PQMN的邊QM在BC上,頂點P,N分別在AB, AC上,若BC=6,AD=4,求正方形PQMN的邊長.
(2)操作:能畫出這類正方形嗎?小波按數學家波利亞在《怎樣解題》中的方法進行操作:如圖2,任意畫△ABC,在AB上任取一點P′,畫正方形P′Q′M′N′,使Q′,M′在BC邊上,N′在△ABC內,連結B N′并延長交AC于點N,畫NM⊥BC于點M,NP⊥NM交AB于點P,PQ⊥BC于點Q,得到四邊形PQMN.小波把線段BN稱為“波利亞線”.
(3)推理:證明圖2中的四邊形PQMN 是正方形.
(4)拓展:在(2)的條件下,于波利業線B N上截取NE=NM,連結EQ,EM(如圖3).當tan∠NBM=![]() 時,猜想∠QEM的度數,并嘗試證明.
時,猜想∠QEM的度數,并嘗試證明.
請幫助小波解決“溫故”、“推理”、“拓展”中的問題.
科目:初中數學 來源: 題型:
【題目】PM2.5是指大氣中直徑小于或等于2.5μm(0.0000025m)的顆粒物,含有大量有毒、有害物質,也稱可入肺顆粒物.將0.0000025用科學記數法表示為
A.25×10﹣7B.2.5×10﹣6C.0.25×10﹣5D.2.5×106
查看答案和解析>>
科目:初中數學 來源: 題型:
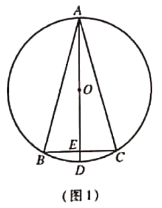
【題目】已知:![]() 是
是![]() 的內接三角形,且
的內接三角形,且![]() ,直徑
,直徑![]() 交
交![]() 于點
于點![]() .
.
![]() 如圖1 ,求證:
如圖1 ,求證:![]() ;
;
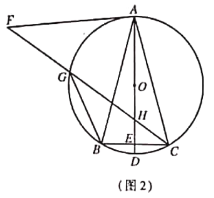
![]() 如圖2,將線段
如圖2,將線段![]() 繞點
繞點![]() 順時針旋轉得到線段
順時針旋轉得到線段![]() ,旋轉角為
,旋轉角為![]() 連接
連接![]() 分別交
分別交![]() ,
,![]() 于點
于點![]() ,連接
,連接![]() ,求證:
,求證: ![]() ;
;
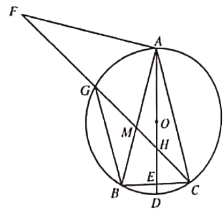
![]() 如圖3,在(2)的條件下,當
如圖3,在(2)的條件下,當![]() 時,
時,![]() 交
交![]() 于點
于點![]() 若
若![]() 求
求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
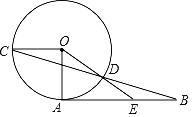
【題目】如圖,AB是⊙O的切線,OA,OC是⊙O的半徑,且OC∥AB,連接BC交⊙O于點D,點D恰為BC的中點,連接OD并延長,交AB于點E.
(1)求∠B的度數;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某書店以![]() 元的價格購進一批科普書進行銷售,物價局根據市場行情規定,銷售單價不低于
元的價格購進一批科普書進行銷售,物價局根據市場行情規定,銷售單價不低于![]() 元且不高于
元且不高于![]() 元.在銷售中發現,該科普書的每天銷售數量
元.在銷售中發現,該科普書的每天銷售數量![]() (本)與銷售單價
(本)與銷售單價![]() (元)之間存在某種函數關系,對應如下:
(元)之間存在某種函數關系,對應如下:
銷售單價 |
|
|
|
|
|
銷售數量 |
|
|
|
|
|
(1)用你所學過的函數知識,求出![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)請問該科普書每天利潤![]() (元)的最大值是多少?
(元)的最大值是多少?
(3)如果該科普書每天利潤必須不少于![]() 元,試求出每天銷售數量
元,試求出每天銷售數量![]() 最少為多少本?
最少為多少本?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 與y軸交于點
與y軸交于點![]() .
.
(1)求c的值;
(2)當![]() 時,求拋物線頂點的坐標;
時,求拋物線頂點的坐標;
(3)已知點![]() ,若拋物線
,若拋物線![]() 與線段
與線段![]() 有兩個公共點,結合函數圖象,求a的取值范圍.
有兩個公共點,結合函數圖象,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com