【題目】請從以下兩個小題中任選一個作答，若多選，則按所選做的第一題計分，
（1）若
，則
______
（2）鐘面上6點20分時，時針與分針所構成的角的度數是______度．
【答案】1 70
【解析】
（1）根據mn=m+3，先化簡2mn+3m-5mn+10，再求出算式的值是多少即可．
（2）因為鐘表上的刻度是把一個圓平均分成了12等份，每一份是30
，借助圖形，找出6點20分時針和分針之間相差的大格數，用大格數乘30即可．
解：
（1）∵mn=m+3，
∴2mn+3m5mn+10=3m3mn+10=3m3(m+3)+10=3m3m9+10=1；
（2）時針在鐘面上每分鐘轉0.5，分針每分鐘轉6，
鐘表上6時20分鐘時，時針與分針的夾角可以看成時針轉過6時0.5×20=10，分針在數字4上，
鐘表12個數字，每相鄰兩個數字之間的夾角為30，
6時20分鐘時分針與時針的夾角2×30+10=70，
故在6點20分，時針和分針的夾角為70；
故答案為：（1）1；（2）70.
同步練習河南大學出版社系列答案
同步練習西南師范大學出版社系列答案科目：初中數學 來源： 題型：
【題目】請仔細閱讀下面兩則材料，然后解決問題：
材料1：小學時我們學過，任何一個假分數都可以化為一個整數與一個真分數的和的形式，同樣道理，任何一個分子次數不低于分母次數的分式都可以化為一個整式與另一個分式的和（或差）的形式，其中分式的分子次數低于分母次數.
如：
.
材料2：對于式子
，利用換元法，令
，
.則由于
，所以反比例函數有最大值，且為3.因此分式的最大值為5.
根據上述材料，解決下列問題：
（1）把分式
化為一個整式與另一個分式的和的形式，其中分式的分子次數低于分母次數.
（2）當
的值變化時，求分式
的最大（或最小）值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】概念學習
規定：如果一個三角形的三個角分別等于另一個三角形的三個角，那么稱這兩個三角形互為“等角三角形”．
從三角形
不是等腰三角形
一個頂點引出一條射線與對邊相交，頂點與交點之間的線段把這個三角形分割成兩個小三角形，如果分得的兩個小三角形中一個為等腰三角形，另一個與原來三角形是“等角三角形”，我們把這條線段叫做這個三角形的“等角分割線”．
理解概念
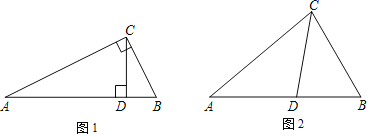
如圖1，在
中，
，
，請寫出圖中兩對“等角三角形”
概念應用
如圖2，在
中，CD為角平分線，
，
．
求證：CD為的等角分割線．
在中，
，CD是的等角分割線，直接寫出
的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
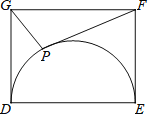
【題目】在△ABC中，若O為BC邊的中點，則必有：AB2+AC2=2AO2+2BO2成立．依據以上結論，解決如下問題：如圖，在矩形DEFG中，已知DE=4，EF=3，點P在以DE為直徑的半圓上運動，則PF2+PG2的最小值為（ ）
A. 
B. 
C. 34 D. 10
查看答案和解析>>
科目：初中數學 來源： 題型：
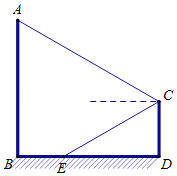
【題目】某游樂場一轉角滑梯如圖所示，滑梯立柱AB、CD均垂直于地面，點E在線段BD上，在C點測得點A的仰角為30°，點E的俯角也為30°，測得B、E間距離為10米，立柱AB高30米．求立柱CD的高（結果保留根號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明家1至6月份的用水量統計如圖所示，關于這組數據，下列說法錯誤的是（ ）．
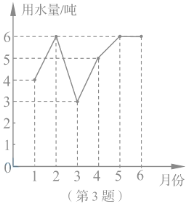
A、眾數是6噸 B、平均數是5噸 C、中位數是5噸 D、方差是
查看答案和解析>>
科目：初中數學 來源： 題型：
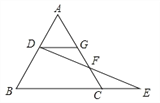
【題目】已知：如圖,點D在等邊△ABC的邊AB上，作DG∥BC，交AC于點G，點F在邊AC上，連接DF并延長，交BC的延長線于點E，FE=FD.求證：AD=CE.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，AB=AC，利用直尺和圓規完成如下操作：
①作∠BAC的平分線交BC于點D；
②作邊AB的垂直平分線EF，EF與AD相交于P點；
③連接PB、PC，
請你觀察所作圖形，解答下列問題：
（1）線段PA、PB、PC之間的大小關系是________；
（2）若∠ABC=68°，求∠BPC的度數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
