
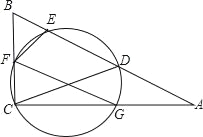
【題目】如圖,D為Rt△ABC斜邊AB上一點,以CD為直徑的圓分別交△ABC三邊于E、F、G三點,連接FE,FG.
(1)求證:∠EFG=∠B;
(2)若AC=2BC=4![]() ,D為AE的中點,求FG的長.
,D為AE的中點,求FG的長.
【答案】(1)證明見解析;(2)4![]()
【解析】試題分析:(1)連接EC,則∠AEC=90°,由同角的余角相等即可得出∠B=∠ECA,再根據圓周角定理即可得出∠ECA=∠EFG,由此即可證出∠EFG=∠B;
(2)由AC、BC的長度利用勾股定理即可求出AB的長度,結合面積法即可得出CE的長度,由正切即可得出AE的長度,再利用勾股定理可求出CD的長度,連接FD、DG,由矩形的判定定理即可證出四邊形FCGD為矩形,利用矩形的性質即可得出FG=CD,此題得解.
試題解析:(1)證明:連接EC,如圖1所示.
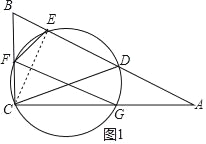
∵CD為直徑,
∴∠AEC=90°,
∴∠BCE+∠B=90°.
∵∠BCE+∠ECA=90°,
∴∠B=∠ECA.
又∵∠ECA=∠EFG,
∴∠EFG=∠B;
(2)解:在Rt△BCA中,AC=4![]() ,BC=2
,BC=2![]() ,
,
∴AB=![]() =10.
=10.
∵BCAC=ABCE,
∴CE=4.
∵tan∠A=![]() ,
,
∴AE=2CE=8.
在Rt△DCG中,CE=4,ED=![]() AE=4,
AE=4,
∴CD=![]() =4
=4![]() .
.
連接FD、DG,如圖2所示.
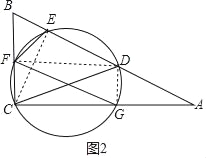
∵CD是直徑,
∴∠CFD=∠CGD=90°,
又∵∠FCG=90°,
∴四邊形FCGD為矩形,
∴FG=CD=4![]() .
.


 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:
【題目】學校準備購買A、B兩種獎品,獎勵成績優異的同學.已知購買1件A獎品和1件B獎品共需18元;購買30件A獎品和20件B獎品共需480元.
(1)A、B兩種獎品的單價分別是多少元?
(2)如果學校購買兩種獎品共100件,總費用不超過850元,那么最多可以購買A獎品多少件.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個三位數,如果把它的個位數字與百位數字交換位置,那么所得的新數比原數小99,且各位數字之和為14,十位數字是個位數字與百位數字之和.求這個三位數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校七年級學生準備去購買《英漢詞典》一書,此書標價為20元。現A、B兩書店都有此書出售,A店按如下方法促銷:若只購一本,則按標價銷售;若一次性購買多于一本,但不多出20本時,每多購一本,每本銷售價在標價的基礎上優惠2%(例如買兩本,每本價優惠2%;買三本價優惠4%,以此類推);若購買多于20本時,每本售價為12元,B店一律按標價的7折銷售;
(1)試分別寫出在兩書店購此書的總價yA、yB與購本書數x之間的函數關系式.
(2)若某班一次性購買多于20本時,那么去哪家書店購買更合算?為什么?若要一次性購買不多于20本時,先寫出y(y=yA-yB)與購書本數x之間的函數關系式,并在圖中畫出其函數圖象,再利用函數圖象分析去哪家書店購買更合算.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線y=m是平行于X軸的直線,將拋物線y=-![]() x2-4x在直線y=m上側的部分沿直線 y=m翻折,翻折后的部分與沒有翻折的部分組成新的函數圖像,若新的函數圖像剛好與 直線y=-x有3個交點,則滿足條件的m 的值為_________
x2-4x在直線y=m上側的部分沿直線 y=m翻折,翻折后的部分與沒有翻折的部分組成新的函數圖像,若新的函數圖像剛好與 直線y=-x有3個交點,則滿足條件的m 的值為_________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一個正整數能表示成兩個連續偶數的平方差,那么這個正整數為“神秘數”.
如:![]()
![]()
![]()
因此,4,12,20這三個數都是神秘數.
(1)28和2012這兩個數是不是神秘數?為什么?
(2)設兩個連續偶數為![]() 和
和![]() (其中
(其中![]() 為非負整數),由這兩個連續偶數構造的神秘數是4的倍數,請說明理由.
為非負整數),由這兩個連續偶數構造的神秘數是4的倍數,請說明理由.
(3)兩個連續奇數的平方差(取正數)是不是神秘數?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數 y=kx+b(k≠0)的圖象經過點(-1,-5),(2,1)兩點.
(1)求 k 和 b 的值;
(2)一次函數 y=kx+b 圖象與坐標軸所圍成的三角形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙中的每個小方格都是邊長為1個單位的正方形,△ABC的頂點均在格點上,直線a為對稱軸,A和C都在對稱軸上.
(1)△ABC以直線a為對稱軸作△AB1C;
(2)若∠BAC=30°,則∠BAB1=______°;
(3)求△ABB1的面積等于______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com