
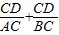 的值是否發生變化,若不變,試求出這個不變的值,若變化,試說明理由.
的值是否發生變化,若不變,試求出這個不變的值,若變化,試說明理由.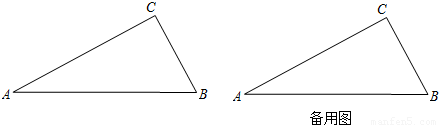
 m,由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得AE=BF,CE=CF,故CA+CB=CE+EA+CB=CE+CF=2CE,在Rt△PCE中,∠PEC=90°,∠PCE=45°,PC=n,可知CE=PE=
m,由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得AE=BF,CE=CF,故CA+CB=CE+EA+CB=CE+CF=2CE,在Rt△PCE中,∠PEC=90°,∠PCE=45°,PC=n,可知CE=PE= n,即CA+CB=2CE=
n,即CA+CB=2CE= n,由△ABC的周長為=AB+BC+CA即可得出其周長,再根據S△ABC=S△PAC+S△PBC-S△PAB即可得出其面積;
n,由△ABC的周長為=AB+BC+CA即可得出其周長,再根據S△ABC=S△PAC+S△PBC-S△PAB即可得出其面積; CD,由平行線分線段成比例定理可知
CD,由平行線分線段成比例定理可知 =
=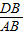 ,
, =
= ,再把兩式相加即可得出結論.
,再把兩式相加即可得出結論. 解:(1)依題意,點P既在∠ACB的平分線上,又在線段AB的垂直平分線上.
解:(1)依題意,點P既在∠ACB的平分線上,又在線段AB的垂直平分線上. ,
,
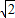 m,
m, n,
n, n,
n, m+
m+ n.
n. AC•PF+
AC•PF+ BC•PF-
BC•PF- PA•PB
PA•PB (AC+BC)•PE-
(AC+BC)•PE- PA2
PA2 ×
× n×
n× n-
n- m2
m2 n2-
n2- m2(n>m).
m2(n>m). AC•BC=
AC•BC= [(AC+BC)2-(AC2+BC2)]=
[(AC+BC)2-(AC2+BC2)]= (n2-m2)]
(n2-m2)]
 CD,
CD, =
= ①;
①; =
= ②,
②, +
+ =
= ,即
,即 +
+ =1
=1 (
( +
+ )=1,即
)=1,即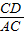 +
+ =
= ;
; AC•BC
AC•BC AC•DM+
AC•DM+ BC•DN=
BC•DN= (AC+BC)•
(AC+BC)• CD
CD (AC+BC)•
(AC+BC)• CD=
CD= AC•BC
AC•BC =
= ,即
,即 +
+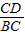 =
= ;
; 【法3】過點D作DN⊥BC,垂足為N(圖4).
【法3】過點D作DN⊥BC,垂足為N(圖4). CD,
CD, =
= ①;
①; =
= ②
② +
+ =
= ,即
,即 +
+ =1
=1 (
( +
+ )=1,即
)=1,即 +
+ =
= ;
;
 BC=
BC= CG.
CG. =
= ,
, =
= ,
, =
= ,
, +
+ =
= ;
; 【法5】過點A作CB的平行線,交射線CD于點K(見圖6),
【法5】過點A作CB的平行線,交射線CD于點K(見圖6), AC,DK=CK-CD=
AC,DK=CK-CD= AC-CD,
AC-CD, =
= ,即
,即 =
= ,
, =
= -
- ,即
,即 +
+ =
= ;
; AC,BG=
AC,BG= BC,
BC, =
= ,
, =
=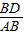
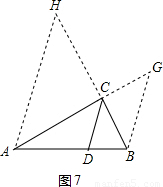
 +
+ =1,
=1, +
+ =1,即
=1,即 +
+ =
= ;
;

 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
 情況;若不可能,請說明理由.
情況;若不可能,請說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖所示,已知△ABC中,AB=AC,以AB為直徑作⊙O交BC于D,交AC于E,過D作DF⊥AC于F
如圖所示,已知△ABC中,AB=AC,以AB為直徑作⊙O交BC于D,交AC于E,過D作DF⊥AC于F查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com