
【題目】如圖,直線OA與直線BC相交于點A,且點B的坐標為(5,﹣1),點C的坐標為(3,1),直線OA的解析式為y=3x
(1)求直線BC的解析式;
(2)求點A的坐標;
(3)求△OAC的面積.
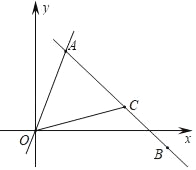
【答案】(1)y=﹣x+4;(2)點A的坐標為(1,3);(3)4.
【解析】
(1)根據點B和點C的坐標可以求得直線BC的解析式;
(2)根據直線OA與直線BC相交于點A,可以求得點A的坐標;
(3)根據直線BC的函數解析式可以求得該直線與x軸的交點坐標,由圖形可知△OAC的面積等于△OAD與△OCD的面積之差,本題得以解決.
解:(1)設直線BC的解析式為y=kx+b,
∵點B的坐標為(5,﹣1),點C的坐標為(3,1),且在直線BC上,
∴![]() ,
,
解得![]() ,
,
即直線BC的解析式為y=﹣x+4;
(2)∵直線OA與直線BC相交于點A,
∴![]() ,
,
解得![]() ,
,
∴點A的坐標為(1,3);
(3)如圖:設直線BC與x軸的交點為點D,
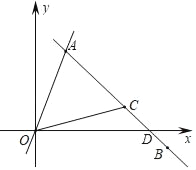
將y=0代入y=﹣x+4,得x=4,
∴點D的坐標作為(4,0),
∴S△OAC= S△OAD- S△OCD=![]() ,
,
即△OAC的面積是4.


科目:初中數學 來源: 題型:
【題目】為了出行方便,現在很多家庭都購買了小汽車.又由于能源緊張和環境保護,石油的市場價格常常波動.為了在價格的波動中盡可能減少損失,常常有兩種加油方案.
方案一:每次加50元的油.方案二:每次加50升的油.
請同學們以2次加油為例(第一次油價為a元/升,第二次油價為b元/升,a>0,b>0且a≠b),計算這兩種方案中,哪種加油方案更實惠便宜(平均單價小的便宜)?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某研究性學習小組為了解同學們上學年參加社會實踐活動的天數,隨機抽查了該市部分八年級學生,來了解上學年參加社會實踐活動的天數,并用得到的數據繪制了如圖兩幅不完整的統計圖![]() 請你根據圖中提供的信息問答下列問題:
請你根據圖中提供的信息問答下列問題:
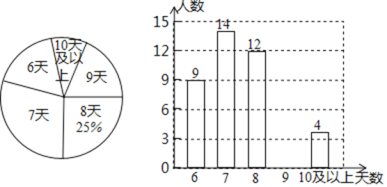
![]() 本次共抽查了多少人?
本次共抽查了多少人?
![]() 補全條形統計圖.
補全條形統計圖.
![]() 在這次調查中,參加社會實踐活動天數的眾數和中位數分別是多少?
在這次調查中,參加社會實踐活動天數的眾數和中位數分別是多少?
![]() 如果本區市共有八年級學生14400人,請你估計“參加社會實踐活動時間不少于9天”的有多少人?
如果本區市共有八年級學生14400人,請你估計“參加社會實踐活動時間不少于9天”的有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】公司投資750萬元,成功研制出一種市場需求量較大的產品,并再投入資金1750萬元進行相關生產設備的改進.已知生產過程中,每件產品的成本為60元.在銷售過程中發現,當銷售單價定為120元時,年銷售量為24萬件;銷售單價每增加10元,年銷售量將減少1萬件.設銷售單價為x(元)(x>120),年銷售量為y(萬件),第一年年獲利(年獲利=年銷售額﹣生產成本)為z(萬元).
(1)求出y與x之間,z與x之間的函數關系式;
(2)該公司能否在第一年收回投資.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列條件:①∠A﹣∠B=∠C; ②∠A:∠B:∠C=2:3:5; ③∠A=![]() ∠B=
∠B= ![]() ∠ C;④∠A=∠B=2∠C;⑤∠A=∠B=
∠ C;④∠A=∠B=2∠C;⑤∠A=∠B= ![]() ∠C,其中能確定△ABC 為直角三角形的條件有 ( )
∠C,其中能確定△ABC 為直角三角形的條件有 ( )
A.2 個B.3 個C.4 個D.5 個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD的對角線AC、BD交于點O,AE平分∠BAD交BC于點E,且∠ADC=60°,AB=![]() BC,連接OE.下列結論:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,連接OE.下列結論:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的個數有( )
BC,成立的個數有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,給出以下結論:
①b2>4ac;
②abc>0;
③2a﹣b=0;
④8a+c<0;
⑤9a+3b+c<0,
其中結論正確有( )個。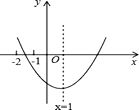
A.2個
B.3個
C.4個
D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線l1∥l2,且l4和l1、l2分別交于A、B兩點,點P為線段AB上.的一個定點(如圖1)

(1)寫出∠1、∠2、∠3、之間的關系并說出理由.
(2)如果點P為線段AB上.的動點時,問∠1、∠2、∠3之間的關系是否發生變化?(不必說理由)
(3)如果點P在A、B兩點外側運動時, (點P和點A、點B不重合)
①如圖2,當點P在射線AB上運動時,∠1、∠2、∠3之間關系并說出理由.
②如圖3,當點P在射線BA上運動時,∠1、∠2、∠3之間關系(不說理由)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com