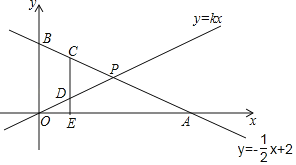
【題目】在平面直角坐標系中，一次函數y＝﹣
x+2的圖象交x軸、y軸分別于A、B兩點，交直線y＝kx于P．
（1）求點A、B的坐標；
（2）若OP＝PA，求k的值；
（3）在（2）的條件下，C是線段BP上一點，CE⊥x軸于E，交OP于D，若CD＝2ED，求C點的坐標．
名校課堂系列答案科目：初中數學 來源： 題型：
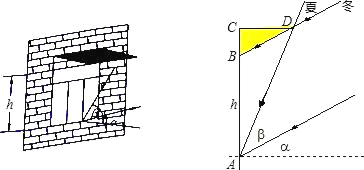
【題目】州政府投資3個億擬建的恩施民族高中，它位于北緯31°，教學樓窗戶朝南，窗戶高度為h米，此地一年的冬至這一天的正午時刻太陽光與地面的夾角最小為α，夏至這一天的正午時刻太陽光與地面的夾角最大為β．若你是一名設計師，請你為教學樓的窗戶設計一個直角形遮陽蓬BCD，要求它既能最大限度地遮擋夏天炎熱的陽光，又能最大限度地使冬天溫暖的陽光射入室內（如圖）．根據測量測得∠α=32.6°，∠β=82.5°，h=2.2米．請你求出直角形遮陽蓬BCD中BC與CD的長各是多少？（結果精確到0.1米）
（參考數據：sin32.6°=0.54，sin82.5°=0.99，tan32.6°=0.64，tan82.5°=7.60）
查看答案和解析>>
科目：初中數學 來源： 題型：
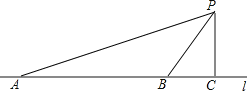
【題目】汽車超速行駛是交通安全的重大隱患，為了有效降低交通事故的發生，許多道路在事故易發路段設置了區間測速如圖，學校附近有一條筆直的公路l，其間設有區間測速，所有車輛限速40千米/小時數學實踐活動小組設計了如下活動：在l上確定A，B兩點，并在AB路段進行區間測速．在l外取一點P，作PC⊥l，垂足為點C．測得PC=30米，∠APC=71°，∠BPC=35°．上午9時測得一汽車從點A到點B用時6秒，請你用所學的數學知識說明該車是否超速．（參考數據：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70，sin71°≈0.95，cos71°≈0.33，tan71°≈2.90）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在半徑為5的⊙O中，弦AB=8，P是弦AB所對的優弧上的動點，連接AP，過點A作AP的垂線交射線PB于點C，當△PAB是等腰三角形時，線段BC的長為______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知AB是⊙O的直徑，點C在⊙O上，過點C的直線與AB的延長線交于點P，AC=PC，∠COB=2∠PCB.
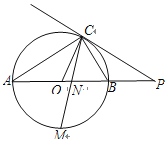
（1）求證：PC是⊙O的切線；
（2）求證：BC=
AB；
（3）點M是弧AB的中點，CM交AB于點N，若AB=4，求MN
MC的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
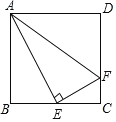
【題目】如圖，在正方形ABCD中，E是BC的中點，F是CD上一點，AE⊥EF．有下列結論：①∠BAE＝30°；②射線FE是∠AFC的角平分線；③AE2＝ADAF；④AF＝AB+CF．其中正確結論為是______．（填寫所有正確結論的序號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，拋物線y=ax22a2x(a
0)的對稱軸與x軸交于點P．
（1）求點P的坐標（用含a的代數式表示）；
（2）記函數y=x+2(1
x2)的圖象為圖形M，若拋物線與圖形M恰有一個公共點，結合函數的圖象，求a的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，方格紙中的每個小方格都是邊長為1個單位的正方形，在建立平面直角坐標系后，△ABC的頂點均在格點上，點B的坐標為（0，1）．
（1）畫出△ABC向右平移3個單位長度所得的△A1B1C1；寫出C1點的坐標；
（2）畫出將△ABC繞點B按逆時針方向旋轉90°所得的△A2B2C2；寫出C2點的坐標；
（3）在（2）的條件下求點A所經過路徑的長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】劉徵是我國古代最杰出的數學家之一，他在《九算術圓田術）中用“割圓術”證明了圓面積的精確公式，并給出了計算圓周率的科學方法（注：圓周率＝圓的周長與該圓直徑的比值）“割圓術”就是以“圓內接正多邊形的面積”，來無限逼近“圓面積”，劉徽形容他的“割圓術”說：割之彌細，所失彌少，割之又割，以至于不可割，則與圓合體，而無所失矣．劉徽計算圓周率是從正六邊形開始的，易知圓的內接正六邊形可分為六個全等的正三角形，每個三角形的邊長均為圓的半徑R．此時圓內接正六邊形的周長為6R，如果將圓內接正六邊形的周長等同于圓的周長，可得圓周率為3．當正十二邊形內接于圓時，如果按照上述方法計算，可得圓周率為_____．（參考數據：sinl5°＝0.26）
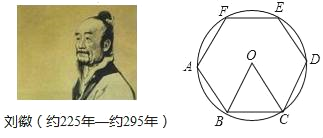
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
