
【題目】中華文明,源遠流長;中華漢字,寓意深廣.為傳承中華優秀傳統文化,某校團委組織了一次全校3000名學生參加的“漢字聽寫”大賽.為了解本次大賽的成績,校團委隨機抽取了其中200名學生的成績作為樣本進行統計,制成如下不完整的統計圖表:

根據所給信息,解答下列問題:
(1)m= ,n= ;
(2)補全頻數分布直方圖;
(3)這200名學生成績的中位數會落在 分數段;
(4)若成績在90分以上(包括90分)為“優”等,請你估計該校參加本次比賽的3000名學生中成績是“優”等的約有多少人?
【答案】(1)70,0.2;(2)補圖見解析;(3)80≤x<90;(4)750人.
【解析】
試題分析:(1)根據第一組的頻數是10,頻率是0.05,求得數據總數,再用數據總數乘以第四組頻率可得m的值,用第三組頻數除以數據總數可得n的值;
(2)根據(1)的計算結果即可補全頻數分布直方圖;
(3)根據中位數的定義,將這組數據按照從小到大的順序排列后,處于中間位置的數據(或中間兩數據的平均數)即為中位數;
(4)利用總數3000乘以“優”等學生的所占的頻率即可.
試題解析:(1)本次調查的總人數為10÷0.05=200,
則m=200×0.35=70,n=40÷200=0.2,
(2)頻數分布直方圖如圖所示,
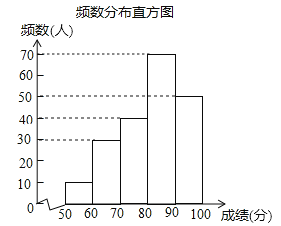
(3)200名學生成績的中位數是第100、101個成績的平均數,而第100、101個數均落在80≤x<90,
∴這200名學生成績的中位數會落在80≤x<90分數段,
(4)該校參加本次比賽的3000名學生中成績“優”等的約有:3000×0.25=750(人).


科目:初中數學 來源: 題型:
【題目】中國數學史上最先完成勾股定理證明的數學家是公元3世紀三國時期的趙爽,他為了證明勾股定理,創制了一副”弦圖“,后人稱其為“趙爽弦圖”(如圖1).圖2由弦圖變化得到,它是由八個全等的直角三角形拼接而成.將圖中正方形MNKT,正方形EFGH,正方形ABCD的面積分別記為S1 , S2 , S3 , 若S1+S2+S3=18,則正方形EFGH的面積為 . 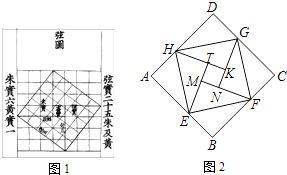
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB與x軸交于點A(1,0),與y軸交于點B(0,﹣2). 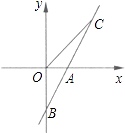
(1)求直線AB的解析式;
(2)若直線AB上的點C在第一象限,且S△BOC=2,求點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=6,BC=4,過對角線BD中點O的直線分別交AB,CD邊于點E,F.
(1)求證:四邊形BEDF是平行四邊形;
(2)當四邊形BEDF是菱形時,求EF的長.
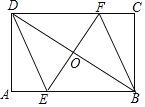
查看答案和解析>>
科目:初中數學 來源: 題型:
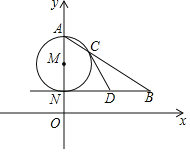
【題目】如圖,AN是⊙M的直徑,NB∥x軸,AB交⊙M于點C.
(1)若點A(0,6),N(0,2),∠ABN=30°,求點B的坐標;
(2)若D為線段NB的中點,求證:直線CD是⊙M的切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】提出問題:如圖1,將三角板放在正方形ABCD上,使三角板的直角頂點P在對角線AC上,一條直角邊經過點B,另一條直角邊交邊DC與點E,求證:PB=PE
分析問題:學生甲:如圖1,過點P作PM⊥BC,PN⊥CD,垂足分別為M,N通過證明兩三角形全等,進而證明兩條線段相等.
學生乙:連接DP,如圖2,很容易證明PD=PB,然后再通過“等角對等邊”證明PE=PD,就可以證明PB=PE了.
解決問題:請你選擇上述一種方法給予證明.
問題延伸:如圖3,移動三角板,使三角板的直角頂點P在對角線AC上,一條直角邊經過點B,另一條直角邊交DC的延長線于點E,PB=PE還成立嗎?若成立,請證明;若不成立,請說明理由.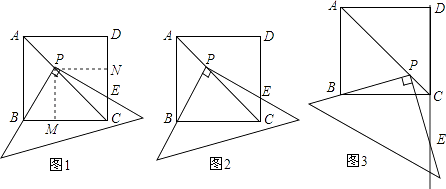
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com