
 解:(1)過D作DH∥AB交BC于H點,
解:(1)過D作DH∥AB交BC于H點,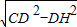 =6,
=6, (AD+BC)AB=
(AD+BC)AB= ×(2+8)×8=40.
×(2+8)×8=40. <4.
<4. 秒時,PQ將梯形ABCD周長平分.
秒時,PQ將梯形ABCD周長平分. =
=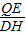 =
=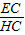 ,
,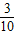 =
=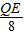 =
=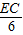 ,
,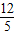 ,EC=
,EC= ,
, =
=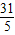 ,
, (PB+QE)×BE+
(PB+QE)×BE+ QE×EC,
QE×EC, ×(
×(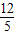 +3)×
+3)×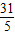 +
+ ×
×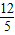 ×
× ,
, ,
,
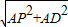 =
=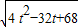 .
. t,QE=
t,QE= t,
t, t,BH=QE=
t,BH=QE= t.
t. t=
t= t.
t.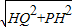 =
= =
=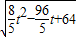 ,
,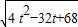 ,
,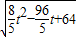 ,
,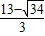 ,t=
,t=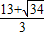 >4(不合題意舍去),
>4(不合題意舍去),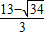 ,
,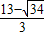 或4,4≤t<5或5<t≤6時,以DQ為腰的等腰△DPQ成立.
或4,4≤t<5或5<t≤6時,以DQ為腰的等腰△DPQ成立.

科目:初中數學 來源: 題型:
 如圖,已知直角梯形ABCD中,AD∥BC∥EF,∠A=90°,BC=DC=4,AC、BD交于E,且EF=ED.
如圖,已知直角梯形ABCD中,AD∥BC∥EF,∠A=90°,BC=DC=4,AC、BD交于E,且EF=ED.查看答案和解析>>
科目:初中數學 來源: 題型:
 21、當我們遇到梯形問題時,我們常用分割的方法,將其轉化成我們熟悉的圖形來解決:
21、當我們遇到梯形問題時,我們常用分割的方法,將其轉化成我們熟悉的圖形來解決:
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.點E是CD的中點,點F是AB上的點,∠ADF=45°,FE=a,梯形ABCD的面積為m.
如圖,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.點E是CD的中點,點F是AB上的點,∠ADF=45°,FE=a,梯形ABCD的面積為m.查看答案和解析>>
科目:初中數學 來源: 題型:
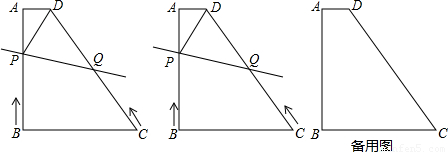
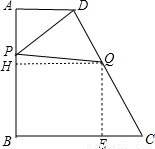
 如圖,已知直角梯形ABCD中,AD∥BC,∠B=90°,∠C=60°,BC=12cm,DC=16cm,動點P沿A→D→C線路以2cm/秒的速度向C運動,動點Q沿B→C線路以1cm/秒的速度向C運動.P、Q兩點分別從A、B同時出發,當其中一點到達C點時,另一點也隨之停止.設運動時間為t秒,△PQB的面積為y cm2.
如圖,已知直角梯形ABCD中,AD∥BC,∠B=90°,∠C=60°,BC=12cm,DC=16cm,動點P沿A→D→C線路以2cm/秒的速度向C運動,動點Q沿B→C線路以1cm/秒的速度向C運動.P、Q兩點分別從A、B同時出發,當其中一點到達C點時,另一點也隨之停止.設運動時間為t秒,△PQB的面積為y cm2.9
| ||
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com