

分析 (1)由題意易知三角形ABE為等腰直角三角形,所以EC=3.當G落在ED上時,可利用△EGH∽△EDC(或tan∠DEC=$\frac{3}{4}$)求出EH的長.求出點H移動的長度,因為G移動的時間等于H移動的時間,問題得解.
(2)在運動過程中,在0<t≤5中,分四種情況進行討論:①0<t≤2時,如圖2,重疊部分是直角三角形,求直角邊JG和KG即可;②2<t≤$\frac{7}{2}$時,如圖3,重疊部分是不規則的多邊形,可利用差來求面積;③$\frac{7}{2}$<t≤4時,如圖4,重疊部分是一梯形與一直角三角形面積的差;④4<t≤5時,如圖5,重疊部分是直角三角形,求直角邊FN和FQ即可;
(3)①當DC旋轉在DE左上方α°時,由圖6知,PD′=PC′-CD′.首先利用勾股定理求出DE,通過直角三角形斜邊與斜邊中線的關系,求出PE的長,再次利用勾股定理求出PC′;②當DE垂直于邊在直角三角形如圖7,利用勾股定理,直接得到關于PC′的二次方程,求出PC′,計算出PD′;③如圖8,當C′P=DP時,在RT△PC′E中利用勾股定理即可.④如圖9,DP=DC′,可得D為PE中點,在RT△PEC′中求出PC′即可解決問題.
解答 解:(1)如圖1,點G落在線段DE上的時,
BE=AB=4,EC=7-4=3,
當G在ED上時,$\frac{EH}{GH}$=$\frac{EC}{DC}$=$\frac{3}{4}$,又GH=2,
∴EH=$\frac{3}{2}$,IE=$\frac{1}{2}$,BI=4-$\frac{1}{2}$=$\frac{7}{2}$
∴t=$\frac{7}{2}$÷1=$\frac{7}{2}$
則點G落在線段DE上的時間t為$\frac{7}{2}$秒;
(2)①0<t≤2時,如圖2,重疊部分是△JKG,
S=S△JKG,
∵BI=t,IH=2,
∴HE=4-2-t=2-t,
∵∠AEB=45°,
∴KH=HE=2-t,
∴JK=GK=2-(2-t)=t,
∴S△JKG=$\frac{1}{2}$JG×GK=$\frac{1}{2}$t2,
∴S=$\frac{1}{2}{t}^{2}$;
②2<t≤$\frac{7}{2}$時,如圖3,重疊部分是五邊形EMGFL,
S=S正方形FGHI-S△LIE-S△EHM,
∵BE=4,BI=t,IE=4-t,
∴LI=IE=4-t,
∴S△LIE=$\frac{1}{2}(4-t)^{2}$.
又EH=IH-IE=2-(4-t)=t-2,
∴MH=$\frac{4}{3}EH$=$\frac{4}{3}$(t-2),
∴S△EHM=$\frac{1}{2}(t-2)$•$\frac{4}{3}(t-2)$=$\frac{2}{3}(t-2)^{2}$,
S=4-$\frac{1}{2}(4-t)^{2}$-$\frac{2}{3}(t-2)^{2}$=-$\frac{7}{6}$t2+$\frac{20}{3}$t-$\frac{20}{3}$;
③$\frac{7}{2}$<t≤4時,如圖4,重疊部分是四邊形ENFL,
S=S梯形IENF-S△EIL,
∵NG=t-$\frac{7}{2}$,
∴FN=2-(t-$\frac{7}{2}$)=$\frac{11}{2}$-t,
又IE=4-t,
∴S梯形IENF=$\frac{1}{2}$[(4-t)+($\frac{11}{2}$-t)]×2=$\frac{19}{2}$-2t,
S△EIL=$\frac{1}{2}$(4-t)2,
∴S=$\frac{19}{2}-2t$-$\frac{1}{2}(4-t)^{2}$=-$\frac{1}{2}{t}^{2}+2t+\frac{3}{2}$;
④4<t≤5時,如圖5,重疊部分是△FQN,
S=S△FQN,
FN=$\frac{11}{2}$-t,FQ=$\frac{4}{3}$FN=$\frac{4}{3}(\frac{11}{2}-t)$,
∴S=$\frac{1}{2}$•$\frac{4}{3}$($\frac{11}{2}-t$)2=$\frac{2}{3}{t}^{2}-\frac{22}{3}t+\frac{121}{6}$
綜上所述:
S=$\left\{\begin{array}{l}{\frac{1}{2}{t}^{2}(0<t≤2)}\\{-\frac{7}{6}{t}^{2}+\frac{20}{3}t-\frac{20}{3}(2<t≤\frac{7}{2})}\\{-\frac{1}{2}{t}^{2}+2t+\frac{3}{2}(\frac{7}{2}<t≤4)}\\{\frac{2}{3}{t}^{2}-\frac{22}{3}t+\frac{121}{6}(4<t≤5)}\end{array}\right.$
(3)①如圖6,當C′D=PD時,
設∠P=∠DC′P=α,
∴∠C′DE=2α,∠C′EP=90°-α,
∴∠DC′E=∠PC′E-∠PC′D=90°-α,
∴C′D=DE,
∴D為EP中點,
∴PE=2DE
∵在RT△CDE中,CE=3,CD=4,
∴ED=5,
∴PE=10,
在RT△C′EP中,
∵C′P2=PE2-C′E2,
∴C′P=$\sqrt{1{0}^{2}-{3}^{2}}$=$\sqrt{91}$,
∴PD′=$\sqrt{91}$-4;
②如圖7,當C′P=DP時,
設C′P=x,則DP=x,PE=DE-DP=5-x
在Rt△EC′P中,(5-x)2=x2+32
x=$\frac{8}{5}$
PD′=4-$\frac{8}{5}$=$\frac{12}{5}$
③如圖8,當C′P=DP時,
PE=5-x,PC′=x
(5-x)2=x2+32,x=$\frac{8}{5}$
∴PD′=C′D′+PC′=4+$\frac{8}{5}$=$\frac{28}{5}$
④如圖9,DP=DC′,可得D為PE中點,
PE=10,C′P=$\sqrt{91}$
PD′=C′D′-C′P=4-$\sqrt{91}$
綜上所述:當△C′DP為等腰三角形時,PD′的長為$\sqrt{91}$-4或$\sqrt{91}$+4或$\frac{12}{5}$或$\frac{28}{5}$.
點評 本題考查幾何變換綜合題、多邊形面積、勾股定理、等腰三角形的判定和性質、分段函數等知識,解題的關鍵是學會分類討論,正確畫出圖形,借助于圖象解決問題,第四個問題有四種情形,不能漏解,屬于中考壓軸題.


科目:初中數學 來源:2016-2017學年山東省淄博市(五四學制)七年級下學期第一次月考數學試卷(解析版) 題型:單選題
一輛汽車在筆直的公路上行駛,兩次拐彎后,仍在原來的方向上平行前進,那么兩次拐彎的角度是( )
A. 第一次右拐50°,第二次左拐130° B. 第一次左拐50°,第二次右拐50°
C. 第一次左拐50°,第二次左拐130° D. 第一次右拐50°,第二次右拐50°
查看答案和解析>>
科目:初中數學 來源:2016-2017學年江蘇省東臺市第六教育聯盟七年級下學期第一次月考數學試卷 題型:單選題
下面有3句話:①同旁內角互補;②兩直線平行,內錯角相等;③在同一平面內,垂直于同一條直線的兩直線互相平行.其中正確的為 ( )
A. ① B. ② C. ③ D. ②③
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
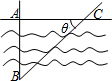 如圖,為了測量河兩岸A、B兩點的距離,在與AB垂直的方向點C處測得AC=a,∠ACB=θ,那么AB等于( )
如圖,為了測量河兩岸A、B兩點的距離,在與AB垂直的方向點C處測得AC=a,∠ACB=θ,那么AB等于( )| A. | a•sinθ | B. | a•tanθ | C. | a•cosθ | D. | $\frac{a}{tanθ}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com