
【題目】如圖,定義:若雙曲線![]() (k>0)與它的其中一條對(duì)稱(chēng)軸y=x相交于A、B兩點(diǎn),則線段AB的長(zhǎng)度為雙曲線
(k>0)與它的其中一條對(duì)稱(chēng)軸y=x相交于A、B兩點(diǎn),則線段AB的長(zhǎng)度為雙曲線![]() (k>0)的對(duì)徑.
(k>0)的對(duì)徑.
(1)求雙曲線![]() 的對(duì)徑.
的對(duì)徑.
(2)若雙曲線![]() (k>0)的對(duì)徑是
(k>0)的對(duì)徑是![]() ,求k的值.
,求k的值.
(3)仿照上述定義,定義雙曲線![]() (k<0)的對(duì)徑.
(k<0)的對(duì)徑.
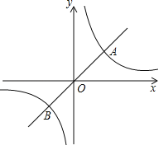
【答案】(1)2![]() (2)25 (3) 若雙曲線
(2)25 (3) 若雙曲線![]() (k<0)與它的其中一條對(duì)稱(chēng)軸y=-x相交于A、B兩點(diǎn),則線段AB的長(zhǎng)稱(chēng)為雙曲線
(k<0)與它的其中一條對(duì)稱(chēng)軸y=-x相交于A、B兩點(diǎn),則線段AB的長(zhǎng)稱(chēng)為雙曲線![]() (k<0)的對(duì)徑
(k<0)的對(duì)徑
【解析】解:如圖,過(guò)A點(diǎn)作AC⊥x軸于C, 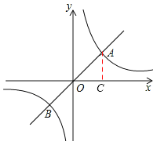
(1)解方程組![]() ,得
,得![]() ,
,
∴A點(diǎn)坐標(biāo)為(1,1),B點(diǎn)坐標(biāo)為(-1,-1)。
∴OC=AC=1,∴OA=![]() OC=
OC=![]() 。∴AB=2OA=2
。∴AB=2OA=2![]() ,
,
∴雙曲線![]() 的對(duì)徑是2
的對(duì)徑是2![]() 。
。
(2)∵雙曲線的對(duì)徑為![]() ,即AB=
,即AB=![]() ,OA=5
,OA=5![]() 。
。
∴OA=![]() OC=
OC=![]() AC,∴OC=AC=5。∴點(diǎn)A坐標(biāo)為(5,5)。
AC,∴OC=AC=5。∴點(diǎn)A坐標(biāo)為(5,5)。
把A(5,5)代入雙曲線![]() (k>0)得k=5×5=25,即k的值為25。
(k>0)得k=5×5=25,即k的值為25。
(3)若雙曲線![]() (k<0)與它的其中一條對(duì)稱(chēng)軸y=-x相交于A、B兩點(diǎn),則線段AB的長(zhǎng)稱(chēng)為雙曲線
(k<0)與它的其中一條對(duì)稱(chēng)軸y=-x相交于A、B兩點(diǎn),則線段AB的長(zhǎng)稱(chēng)為雙曲線![]() (k<0)的對(duì)徑。
(k<0)的對(duì)徑。
過(guò)A點(diǎn)作AC⊥x軸于C,
(1)解方程組![]() ,可得到A點(diǎn)坐標(biāo)為(1,1),B點(diǎn)坐標(biāo)為(-1,-1),即OC=AC=1,由勾股定理可求AB,于是得到雙曲線
,可得到A點(diǎn)坐標(biāo)為(1,1),B點(diǎn)坐標(biāo)為(-1,-1),即OC=AC=1,由勾股定理可求AB,于是得到雙曲線![]() 的對(duì)徑。
的對(duì)徑。
(2)根據(jù)雙曲線的對(duì)徑的定義得到當(dāng)雙曲線的對(duì)徑為![]() ,即AB=
,即AB=![]() ,OA=5
,OA=5![]() ,根據(jù)OA=
,根據(jù)OA=![]() OC=
OC=![]() AC,則OC=AC=5,得到點(diǎn)A坐標(biāo)為(5,5),把A(5,5)代入雙曲線
AC,則OC=AC=5,得到點(diǎn)A坐標(biāo)為(5,5),把A(5,5)代入雙曲線![]() (k>0)即可得到k的值;
(k>0)即可得到k的值;
(3)雙曲線![]() (k<0)的一條對(duì)稱(chēng)軸與雙曲線有兩個(gè)交點(diǎn),根據(jù)題目中的定義易得到雙曲線
(k<0)的一條對(duì)稱(chēng)軸與雙曲線有兩個(gè)交點(diǎn),根據(jù)題目中的定義易得到雙曲線![]() (k<0)的對(duì)徑。
(k<0)的對(duì)徑。


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為加強(qiáng)校園文化建設(shè),某校準(zhǔn)備打造校園文化墻,需用甲、乙兩種石材經(jīng)市場(chǎng)調(diào)查,甲種石材的費(fèi)用![]() (元)與使用面積
(元)與使用面積![]()
![]() 間的函數(shù)關(guān)系如圖所示,乙種石材的價(jià)格為每平方米
間的函數(shù)關(guān)系如圖所示,乙種石材的價(jià)格為每平方米![]() 元.
元.

(1)求![]() 與
與![]() 間的函數(shù)解析式;
間的函數(shù)解析式;
(2)若校園文化墻總面積共![]() ,其中使用甲石材
,其中使用甲石材![]()
![]() ,設(shè)購(gòu)買(mǎi)兩種石材的總費(fèi)用為
,設(shè)購(gòu)買(mǎi)兩種石材的總費(fèi)用為![]() 元,請(qǐng)直接寫(xiě)出
元,請(qǐng)直接寫(xiě)出![]() 與
與![]() 間的函數(shù)解析式;
間的函數(shù)解析式;
(3)在(2)的前提下,若甲種石材使用面積多于![]() ,且不超過(guò)乙種石材面積的
,且不超過(guò)乙種石材面積的![]() 倍,那么應(yīng)該怎樣分配甲、乙兩種石材的面積才能使總費(fèi)用最少?最少總費(fèi)用為多少元?
倍,那么應(yīng)該怎樣分配甲、乙兩種石材的面積才能使總費(fèi)用最少?最少總費(fèi)用為多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,△ABC三個(gè)頂點(diǎn)的坐標(biāo)分別為A(1,1),B(4,2),C(3,4).

(1)請(qǐng)畫(huà)出△ABC向左平移5個(gè)單位長(zhǎng)度后得到的△A1B1C1;
(2)請(qǐng)畫(huà)出△ABC關(guān)于原點(diǎn)對(duì)稱(chēng)的△A2B2C2;
(3)在x軸上求作一點(diǎn)P,使△PAB的周長(zhǎng)最小,請(qǐng)畫(huà)出△PAB,并直接寫(xiě)出P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】“中國(guó)制造”是世界上認(rèn)知度最高的標(biāo)簽之一,因此,我縣越來(lái)越多的群眾選擇購(gòu)買(mǎi)國(guó)產(chǎn)空調(diào),已知購(gòu)買(mǎi)1臺(tái)A型號(hào)的空調(diào)比1臺(tái)B型號(hào)的空調(diào)少200元,購(gòu)買(mǎi)2臺(tái)A型號(hào)的空調(diào)與3臺(tái)B型號(hào)的空調(diào)共需11200元,求A、B兩種型號(hào)的空調(diào)的購(gòu)買(mǎi)價(jià)各是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】我國(guó)南水北調(diào)中線工程的起點(diǎn)是丹江口水庫(kù),按照工程計(jì)劃,需對(duì)原水庫(kù)大壩進(jìn)行混凝土培厚加高,使壩高由原來(lái)的162米增加到176.6米,以抬高蓄水位,如圖是某一段壩體加高工程的截面示意圖,其中原壩體的高為BE,背水坡坡角∠BAE=68°,新壩體的高為DE,背水坡坡角∠DCE=60°.求工程完工后背水坡底端水平方向增加的寬度AC.(結(jié)果精確到0.1米,參考數(shù)據(jù):sin 68°≈0.93,cos 68°≈0.37,tan 68°≈2.5,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】有兩個(gè)相鄰內(nèi)角互余的四邊形稱(chēng)為鄰余四邊形,這兩個(gè)角的夾邊稱(chēng)為鄰余線.
(1)如圖1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的角平分線,
的角平分線,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 上的點(diǎn).求證:四邊形
上的點(diǎn).求證:四邊形![]() 是鄰余四邊形;
是鄰余四邊形;
(2)如圖2,已知![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 的垂直平分線上,
的垂直平分線上,![]() 在邊
在邊![]() 上,
上,![]() 是
是![]() 內(nèi)一點(diǎn), 連接
內(nèi)一點(diǎn), 連接![]() ,
,![]() ,
,![]() ,
,![]() ,若四邊形
,若四邊形![]() 是鄰余四邊形,
是鄰余四邊形,![]() 是鄰余線.
是鄰余線.
①![]() 與
與![]() 有什么位置關(guān)系?說(shuō)明理由.
有什么位置關(guān)系?說(shuō)明理由.
②判斷![]() 形狀,說(shuō)明理由.
形狀,說(shuō)明理由.
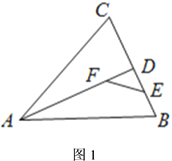

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在某市實(shí)施城中村改造的過(guò)程中,“旺鑫”拆遷工程隊(duì)承包了一項(xiàng)10000 m2的拆遷工程.由于準(zhǔn)備工作充分,實(shí)際拆遷效率比原計(jì)劃提高了25%,提前2天完成了任務(wù),請(qǐng)解答下列問(wèn)題:
(1)求“旺鑫”拆遷工程隊(duì)現(xiàn)在平均每天拆遷多少平方米;
(2)為了盡量減少拆遷給市民帶來(lái)的不便,在拆遷工作進(jìn)行了2天后,“旺鑫”拆遷工程隊(duì)的領(lǐng)導(dǎo)決定加快拆遷工作,將余下的拆遷任務(wù)在5天內(nèi)完成,那么“旺鑫”拆遷工程隊(duì)平均每天至少再多拆遷多少平方米?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,等邊三角形ABC的邊長(zhǎng)為4,AD是BC邊上的中線,F是AD邊上的動(dòng)點(diǎn),E是AC邊上一點(diǎn).若AE=2,當(dāng)EF+CF取得最小值時(shí),∠ECF的度數(shù)為( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,二次函數(shù)![]() 的圖象與
的圖象與![]() 軸正半軸相交,其頂點(diǎn)坐標(biāo)為
軸正半軸相交,其頂點(diǎn)坐標(biāo)為![]() ,下列結(jié)論:①
,下列結(jié)論:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 有兩個(gè)相等的實(shí)數(shù)根,其中正確的結(jié)論是________.(只填序號(hào)即可).
有兩個(gè)相等的實(shí)數(shù)根,其中正確的結(jié)論是________.(只填序號(hào)即可).
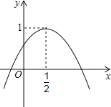
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com