
【題目】如圖,在△ABC中,∠C= 90°,D是BC邊上一點,以DB為直徑的⊙O經過AB的中點E,交AD的延長線于點F,連接EF.
(1)求證:∠1= ∠F;
(2)若CD= 3,EF=![]() ,求⊙O的半徑長.
,求⊙O的半徑長.

【答案】(1)見解析;(2)![]()
【解析】試題分析:(1)連接DE,由BD是⊙O的直徑,得到∠DEB=90°,由于E是AB的中點,得到DA=DB,根據等腰三角形的性質得到∠1=∠B等量代換即可得到結論;
(2)由(1)知,AE=EF,AD=BD,AB=![]() ,設BD=a,則在Rt△ABC和Rt△ACD中,根據勾股定理可得(
,設BD=a,則在Rt△ABC和Rt△ACD中,根據勾股定理可得(![]() )2﹣(a+3)2=a2﹣32,解方程即可得.
)2﹣(a+3)2=a2﹣32,解方程即可得.
試題解析:(1)連接DE,
∵BD是⊙O的直徑,∴∠DEB=90°,
∵E是AB的中點,∴DA=DB,
∴∠1=∠B,
∵∠B=∠F,
∴∠1=∠F;
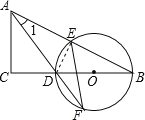
(2)由(1)知,AE=EF,AD=BD,AB=![]() ,
,
在Rt△ABC中,AB2-BC2=AC2,
在Rt△ACD中,AD2-CD2=AC2,
所以AB2-BC2= AD2-CD2,
設BD=a,則(![]() )2﹣(a+3)2=a2﹣32,
)2﹣(a+3)2=a2﹣32,
a=﹣8(舍)或a=5,
∴半徑為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,某校教學樓AB后方有一斜坡,已知斜坡CD的長為12米,坡角α為60°,根據有關部門的規定,∠α≤39°時,才能避免滑坡危險,學校為了消除安全隱患,決定對斜坡CD進行改造,在保持坡腳C不動的情況下,學校至少要把坡頂D向后水平移動多少米才能保證教學樓的安全?(結果取整數)
(參考數據:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個少年在綠茵場上游戲.小紅從點A出發沿線段AB運動到點B,小蘭從點C出發,以相同的速度沿⊙O逆時針運動一周回到點C,兩人的運動路線如圖1所示,其中AC![]() DB.兩人同時開始運動,直到都停止運動時游戲結束,其間他們與點C的距離y與時間x(單位:秒)的對應關系如圖2所示.則下列說法正確的是( )
DB.兩人同時開始運動,直到都停止運動時游戲結束,其間他們與點C的距離y與時間x(單位:秒)的對應關系如圖2所示.則下列說法正確的是( )


A. 小紅的運動路程比小蘭的長
B. 兩人分別在1.09秒和7.49秒的時刻相遇
C. 當小紅運動到點D的時候,小蘭已經經過了點D
D. 在4.84秒時,兩人的距離正好等于⊙O的半徑
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題①如果a,b,c為一組勾股數,那么4a,4b,4c仍是勾股數;②如果三角形的三個內角的度數比是3:4:5,那么這個三角形是直角三角形;③如果一個三角形的三邊是12、25、21,那么此三角形必是直角三角形;④一個等腰直角三角形的三邊是a,b,c,(a>b=c),那么a2:b2:c2=2:1:1.其中正確的是( )
A.①②B.①③C.①④D.②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】不透明的袋子中裝有大小、質地完全相同的2個白球和2個黑球.
(1) 先從袋中投出1個球后放回,混合均勻后再摸出1個球,則第一次摸到白球,第二次摸到黑球的概率為P1為__________;
(2) 若第一次從袋子中摸出1個球后不放回,第二次再摸出1個球,則兩次摸到的球中有1個白球和1個黑球的概率P2是多少?(請用畫樹形圖或列表法求出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
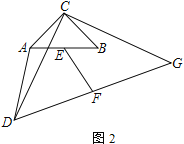
【題目】以C為直角頂點的兩個等腰直角△CAB和△CDG,E為AB的中點,F為DG的中點.
(1)如圖1,點A、B分別在邊CD,CG上,則EF與AD的數量關系是______________;
(2)如圖2,點A、B不在邊CD、CG上,(1)中EF與AD的關系還成立嗎?請證明你的結論;
(3)如圖3,若A、B、G在同一直線上,且A、C、B、F在同一圓上,直接寫出△CDG與△CAB面積之比.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在學習絕對值后,我們知道,![]() 表示數a在數軸上的對應點與原點的距離,如:5表示5在數軸上的對應點到原點的距離.而
表示數a在數軸上的對應點與原點的距離,如:5表示5在數軸上的對應點到原點的距離.而![]() ,即
,即![]() 表示5、0在數軸上對應的兩點之間的距離,類似的,有:
表示5、0在數軸上對應的兩點之間的距離,類似的,有:![]() 表示5、3在數軸上對應的兩點之間的距離;
表示5、3在數軸上對應的兩點之間的距離;![]() ,所以
,所以![]() 表示5、-3在數軸上對應的兩點之間的距離一般地,點A、B在數軸上分別表示有理數a、b,那么A、B之間的距離可表示為
表示5、-3在數軸上對應的兩點之間的距離一般地,點A、B在數軸上分別表示有理數a、b,那么A、B之間的距離可表示為![]() .
.
請根據絕對值的意義并結合數軸解答下列問題:
(1)數軸上表示2和3的兩點之間的距離是________;數軸上P、Q兩點的距離為3,點P表示的數是2,則點Q表示的數是________.
(2)點A、B、C在數軸上分別表示有理數x、-3、1,那么A到B的距離與A到C的距離之和可表示為________(用含絕對值的式子表示);滿足![]() 的x的值為________;
的x的值為________;
(3)試求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABC中,高AD、BE相交于點O,AE=BE,BC=5,且BD=![]() CD.
CD.
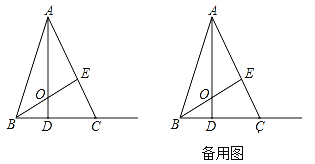
(1)①求證:△AOE≌△BCE;②求線段AO的長.
(2)動點P從點O出發,沿線段OA以每秒1個單位長度的速度向終點A運動,動點Q從點B出發沿射線BC以每秒4個單位長度的速度運動,P、Q兩點同時出發,當點P到達A點時,P、Q兩點同時停止運動.設點P的運動時間為t秒,△POQ的面積為S,請用含t的式子表示S,并直接寫出t相應的的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
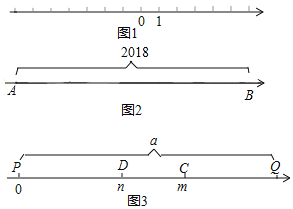
【題目】已知在紙面上有一數軸(如圖1),折疊紙面.
(1)若1表示的點與﹣1表示的點重合,則﹣4表示的點與 表示的點重合;
(2)若﹣2表示的點與8表示的點重合,回答以下問題:
①16表示的點與 表示的點重合;
②如圖2,若數軸上A、B兩點之間的距離為2018(A在B的左側),且A、B兩點經折疊后重合,則A、B兩點表示的數分別是 、 .
(3)如圖3,若m和n表示的點C和點D經折疊后重合,(m>n>0),現數軸上P、Q兩點之間的距離為a(P在Q的左側),且P、Q兩點經折疊后重合,求P、Q兩點表示的數分別是多少?(用含m,n,a的代數式表示)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com