
【題目】已知關(guān)于x的方程kx2﹣2(k+1)x+k﹣1=0有兩個不相等的實數(shù)根.
(1)求k的取值范圍.
(2)是否存在實數(shù)k,使此方程的兩個實數(shù)根的倒數(shù)和等于1?若存在,求出k的值:若不存在,說明理由.
【答案】(1)k>﹣![]() 且k≠0;(2)不存在,理由見解析.
且k≠0;(2)不存在,理由見解析.
【解析】
(1)根據(jù)一元二次方程根的判別式、一元二次方程的定義,即可得到答案;
(2)根據(jù)一元二次方程根與系數(shù)的關(guān)系列出方程,解方程即可.
(1)∵方程kx2﹣2(k+1)x+k﹣1=0有兩個不相等的實數(shù)根,
∴4(k+1)2﹣4k(k﹣1)>0,
即:12k+4>0,
解得,k>﹣![]() ,
,
又∵關(guān)于x的方程kx2﹣2(k+1)x+k﹣1=0是一元二次方程,
∴k≠0,
∴k>﹣![]() 且k≠0;
且k≠0;
(2)不存在,理由如下:
設(shè)關(guān)于x的方程kx2﹣2(k+1)x+k﹣1=0的兩個根分別是:x1,x2.
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
假設(shè):![]() ,即:
,即:![]() ,
,
解得:k=﹣3,
∵k>﹣![]() 且k≠0時,方程有兩個不相等的實數(shù)根,
且k≠0時,方程有兩個不相等的實數(shù)根,
∴不存在實數(shù)k,使此方程的兩個實數(shù)根的倒數(shù)和等于1.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】菲爾茲獎是國際上享有崇高聲譽(yù)的一個數(shù)學(xué)獎項,每4年評選一次,頒給有卓越貢獻(xiàn)的年輕數(shù)學(xué)家,被視為數(shù)學(xué)界的諾貝爾獎.下面的數(shù)據(jù)是從1936年至2014年45歲以下菲爾茲獎得住獲獎時的年齡(歲):39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37 34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38 34 33 40 36 36 37 31 38 38 37 35 40 39 37
請根據(jù)以上數(shù)據(jù),解答以下問題:
(1)小彬按“組距為5”列出了如下的頻數(shù)分布表,每組數(shù)據(jù)含最小值不含最大值,請將表中空缺的部分補(bǔ)充完整,并補(bǔ)全頻數(shù)分布直方圖:
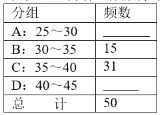
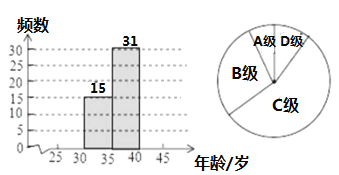
(2)在(1)的基礎(chǔ)上,小彬又畫出了如圖所示的扇形統(tǒng)計圖,圖中B組所對的圓心角的度數(shù)為 ;
(3)根據(jù)(1)中的頻數(shù)分布直方圖試描述這50位菲爾茲獎得主獲獎時的年齡的分布特征.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
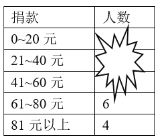
【題目】某校初三(1)班的同學(xué)踴躍為“雅安蘆山地震”捐款,根據(jù)捐款情況(捐款數(shù)為正數(shù))制作以下統(tǒng)計圖表,但生活委員不小心把墨水滴在統(tǒng)計表上,部分?jǐn)?shù)據(jù)看不清楚.
(1)全班有多少人捐款?
(2)如果捐款0~20元的人數(shù)在扇形統(tǒng)計圖中所占的圓心角為72°,那么捐款21~40元的有多少人?
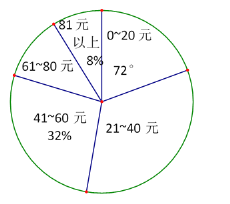
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖是二次函數(shù)y=ax2+bx+c(a,b,c是常數(shù),a≠0)圖象的一部分,與x軸的交點A在點(2,0)和(3,0)之間,對稱軸是x=1.對于下列說法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m為實數(shù));⑤當(dāng)﹣1<x<3時,y>0,其中正確的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
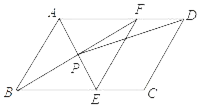
【題目】如圖,ABCD中,點E,F分別是BC和AD邊上的點,AE垂直平分BF,交BF于點P,連接EF,PD.
(1)求證:平行四邊形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
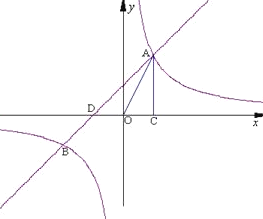
【題目】如圖,已知反比例函數(shù)![]() (k1>0)與一次函數(shù)
(k1>0)與一次函數(shù)![]() 相交于A、B兩點,AC⊥x軸于點C. 若△OAC的面積為1,且tan∠AOC=2 .
相交于A、B兩點,AC⊥x軸于點C. 若△OAC的面積為1,且tan∠AOC=2 .
(1)求出反比例函數(shù)與一次函數(shù)的解析式;
(2)請直接寫出B點的坐標(biāo),并指出當(dāng)x為何值時,反比例函數(shù)y1的值大于一次函數(shù)y2的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
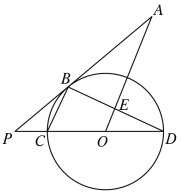
【題目】如圖,已知點![]() 是
是![]() 外一點,直線
外一點,直線![]() 與
與![]() 相切于點
相切于點![]() ,直線
,直線![]() 分別交
分別交![]() 于點
于點![]() 、
、![]() ,
,![]() ,
,![]() 交
交![]() 于點
于點![]() .
.
(1)求證:![]() ;
;
(2)當(dāng)![]() 的半徑為
的半徑為![]() ,
,![]() 時,求
時,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
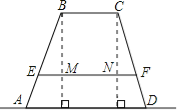
【題目】某高中學(xué)校為高一新生設(shè)計的學(xué)生板凳的正面視圖如圖所示,其中BA=CD,BC=20cm,BC、EF平行于地面AD且到地面AD的距離分別為40cm、8cm.為使板凳兩腿底端A、D之間的距離為50cm,那么橫梁EF應(yīng)為多長?(材質(zhì)及其厚度等暫忽略不計).
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com