Question

已知△ABC中，AB＝，AC＝，BC＝6．

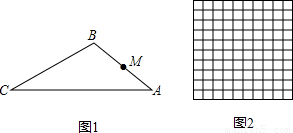
(1)如圖1，點M為AB的中點，在線段AC上取點N，使△AMN與△ABC相似，求線段MN的長；

(2)如圖2，是由100個邊長為1的小正方形組成的10×10的正方形網格，設頂點在這些小正方形頂點

的三角形為格點三角形．

①請你在所給的網格中畫出格點△A₁B₁C₁與△ABC全等(畫出一個即可，不需證明)；

②試直接寫出所給的網格中與△ABC相似且面積最大的格點三角形的個數，并畫出其中一個(不需

證明)．

 

Answer 1

【答案】

解：（1）①如圖A，過點M作MN∥BC交AC于點N，

 則△AMN∽△ABC，

 

 

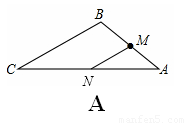
∵M為AB中點，∴MN是△ABC 的中位線。

∵BC＝6，∴MN=3。

②如圖B，過點M作∠AMN=∠ACB交AC于點N，

 

 

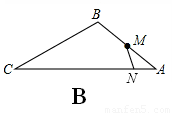
則△AMN∽△ACB，∴。

∵BC=6，AC= 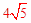 ，AM=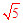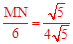，∴，解得MN=。

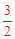綜上所述，線段MN的長為3或。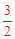

（2）①如圖所示：

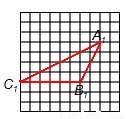
②每條對角線處可作4個三角形與原三角形相似，那么共有8個。

【解析】網格問題，作圖（相似變換），三角形中位線定理，相似三角形的性質。

（1）作MN∥BC交AC于點N，利用三角形的中位線定理可得MN的長；作∠AMN=∠B，利用相似可得MN的長。

（2）①A₁B₁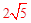＝為直角三角形斜邊的兩直角邊長為2，4，A₁C₁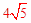＝為直角三角形斜邊的兩直角邊長為4，8。以此，先作B₁C₁＝6，畫出△A₁B₁C₁。

②以所給網格的對角線作為原三角形中最長的邊，可得每條對角線處可作4個三角形與原三角形相似，那么共有8個。