
定義:把一個半圓與拋物線的一部分合成封閉圖形,我們把這個封閉圖形稱為“蛋圓”.如果一條直線與“蛋圓”只有一個交點,那么這條直線叫做“蛋圓”的切線.如圖,A,B,C,D分別是“蛋圓”與坐標軸的交點,已知點D的坐標為(0,8),AB為半圓的直徑,半圓的圓心M的坐標為(1,0),半圓半徑為3.
(1)請你直接寫出“蛋圓”拋物線部分的解析式 ,自變量的取值范圍是 ;
,自變量的取值范圍是 ;
(2)請你求出過點C的“蛋圓”切線與x軸的交點坐標;
(3)求經過點D的“蛋圓”切線的解析式.
(1) 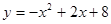 ,
,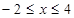 ;(2)(-8.,0);(3)
;(2)(-8.,0);(3) .
.
解析試題分析:(1)由條件知A(-2,0)B(4,0)D(0,8),設y=a(x+2)(x-4),把D點坐標代入即可求出a的值,從而函數解析式可求;
(2)連接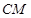 ,設過點C的“蛋圓”切線與x軸的交點為
,設過點C的“蛋圓”切線與x軸的交點為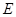 .求出OE長即可.
.求出OE長即可.
(3)(3)設過點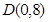 ,“蛋圓”切線的解析式為
,“蛋圓”切線的解析式為 .
.
由題意得,方程組 只有一組解,即
只有一組解,即 有兩個相等實根,
有兩個相等實根,
解得: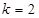
∴過點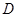 “蛋圓”切線的解析式為
“蛋圓”切線的解析式為 .
.
試題解析:(1)“蛋圓”拋物線部分的解析式為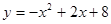 自變量的取值范圍是
自變量的取值范圍是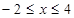 ;
;
(2)如圖,連接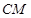 ,設過點C的“蛋圓”切線與x軸的交點為
,設過點C的“蛋圓”切線與x軸的交點為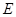 .
.
∴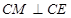 .
.
∵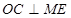 ,
,
在 中,∵
中,∵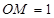 ,
,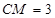 ,
,
∴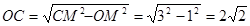 ,
,
∵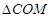 ∽
∽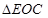 ,
,
∴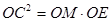 ,∴
,∴ .
.
∴點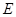 的坐標為(-8.,0).
的坐標為(-8.,0).
(3)設過點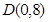 ,“蛋圓”切線的解析式為
,“蛋圓”切線的解析式為 .
.
由題意得,方程組 只有一組解,即
只有一組解,即 有兩個相等實根,
有兩個相等實根,
∴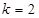
∴過點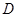 “蛋圓”切線的解析式為
“蛋圓”切線的解析式為 .
.
考點: 二次函數綜合題.


科目:初中數學 來源: 題型:解答題
小明利用暑假20天(8月5日至24日)參與了一家網店經營的社會實踐.負責在網絡上銷售一種新款的SD卡,每張成本價為20元.第 天銷售的相關信息如下表所示.
天銷售的相關信息如下表所示.
| 銷售量p(張) |  |
| 銷售單價q(元/張) |  |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知二次函數 .
.
(1)證明:不論 取何值,該函數圖象與
取何值,該函數圖象與 軸總有兩個公共點;
軸總有兩個公共點;
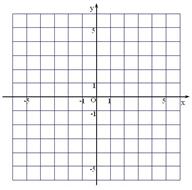
(2)若該函數的圖象與 軸交于點(0,5),求出頂點坐標,并畫出該函數圖象.
軸交于點(0,5),求出頂點坐標,并畫出該函數圖象.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線y=-x2+(m-1)x+m與y軸交于(0,3)點,
(1)求出這條拋物線;
(2)求它與x軸的交點和拋物線頂點的坐標;
(3)x取什么值時,拋物線在x軸上方?
(4)x取什么值時,y的值隨x的增大而減小?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線 與x軸交于A、C兩點,與y軸交于B點.
與x軸交于A、C兩點,與y軸交于B點.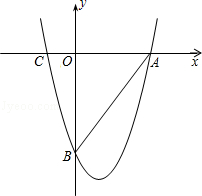
(1)求△AOB的外接圓的面積;
(2)若動點P從點A出發,以每秒1個單位沿射線AC方向運動;同時,點Q從點B出發,以每秒0.5個單位沿射線BA方向運動,當點P到達點C處時,兩點同時停止運動.問當t為何值時,以A、P、Q為頂點的三角形與△OAB相似?
(3)若M為線段AB上一個動點,過點M作MN平行于y軸交拋物線于點N.
問:是否存在這樣的點M,使得四邊形OMNB恰為平行四邊形?若存在,求出點M的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知:拋物線y=ax2+bx+c(a>0)的圖象經過點B(12,0)和C(0,-6),對稱軸為x=2.
(1)求該拋物線的解析式;
(2)點D在線段AB上且AD=AC,若動點P從A出發沿線段AB以每秒1個單位長度的速度勻速運動,同時另一動點Q以某一速度從C出發沿線段CB勻速運動,問是否存在某一時刻,使線段PQ被直線CD垂直平分?若存在,請求出此時的時間t(秒)和點Q的運動速度;若不存在,請說明理由;
(3)在(2)的結論下,直線x=1上是否存在點M,使△MPQ為等腰三角形?若存在,請求出所有點M的坐標;若不存在請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
(1)已知二次函數 ,請你化成
,請你化成 的形式,并在直角坐標系中畫出
的形式,并在直角坐標系中畫出 的圖象;
的圖象;
(2)如果 ,
, 是(1)中圖象上的兩點,且
是(1)中圖象上的兩點,且 ,請直接寫出
,請直接寫出 、
、 的大小關系;
的大小關系;
(3)利用(1)中的圖象表示出方程 的根來,要求保留畫圖痕跡,說明結果.
的根來,要求保留畫圖痕跡,說明結果.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
為鼓勵大學畢業生自主創業,某市政府出臺了相關政策:由政府協調,本市企業按成本價提供產品給大學畢業生自主銷售,成本價與出廠價之間的差價由政府承擔.李明按照相關政策投資銷售本市生產的一種新型節能燈.已知這種節能燈的成本價為每件10元,出廠價為每件12元,每月銷售量y(件)與銷售單價x(元)之間的關系近似滿足一次函數:y=﹣10x+500.
(1)李明在開始創業的第一個月將銷售單價定為20元,那么政府這個月為他承擔的總差價為多少元?
(2)設李明獲得的利潤為w(元),當銷售單價定為多少元時,每月可獲得最大利潤?
(3)物價部門規定,這種節能燈的銷售單價不得高于25元.如果李明想要每月獲得的利潤不低于3000元,那么政府為他承擔的總差價最少為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com