Question

【題目】如圖所示，在一次夏令營活動中，小明從營地A點出發，沿北偏東60°方向走了5 km到達B點，然后再沿北偏西30°方向走了5km到達目的地C點．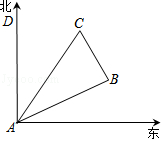
（1）求A、C兩點之間的距離；
（2）確定目的地C在營地A的什么方向上．

Answer 1

【答案】
（1）解：過B點作直線EF∥AD

，

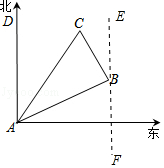∴∠DAB=∠ABF=60°，

∵∠EBC=30°，

∴∠ABC=180°﹣∠ABF﹣∠EBC=180°﹣60°﹣30°=90°，

∴△ABC為直角三角形，由已知可得：BC=5km，AB=5 km，

由勾股定理可得：AC2=BC2+AB2，

所以AC= =10（km），

即：A、C兩點之間的距離為10km

（2）解：在Rt△ABC中，∵BC=5km，AC=10km，

∴∠CAB=30°，

∵∠DAB=60°，

∴∠DAC=30°，

即點C在點A的北偏東30°的方向上

【解析】（1）根據平行線的性質，可得∠ABF，根據直角三角形的判定，可得∠ABC，根據勾股定理，可得答案；（2）根據直角三角形的性質，可得∠CAB，根據角的和差，可得答案．