
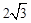 ,若以O為坐標原點,OA所在直線為x軸,建立如圖所示的平面直角坐標系,點B在第一象限內,將Rt△OAB沿OB折疊后,點A落在第一象限內的點C處.
,若以O為坐標原點,OA所在直線為x軸,建立如圖所示的平面直角坐標系,點B在第一象限內,將Rt△OAB沿OB折疊后,點A落在第一象限內的點C處.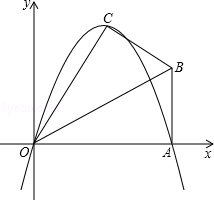
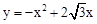
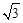 ,1)
,1)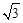 求出y的值,即可得出D點坐標。
求出y的值,即可得出D點坐標。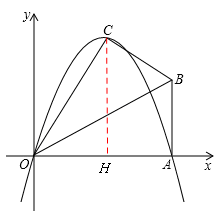
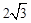 ,
,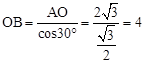 ,AB=2。
,AB=2。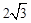 ,
,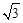 ,CH=3。
,CH=3。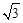 ,3)。
,3)。 (a≠0)。
(a≠0)。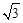 ,3)、A(
,3)、A(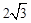 ,0)兩點,
,0)兩點, ,解得
,解得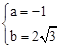 。
。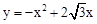 。
。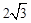 ,AB=2,∴B點坐標為(
,AB=2,∴B點坐標為(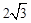 ,2)。
,2)。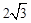 k,解得:k=
k,解得:k=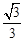 。
。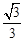 x。
x。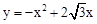 的對稱軸為直線
的對稱軸為直線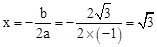 ,
,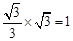 。
。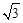 ,1)。
,1)。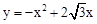 的頂點坐標為(
的頂點坐標為(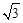 ,3),即為點C,
,3),即為點C,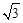 t。∴P(
t。∴P(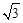 t,t)。
t,t)。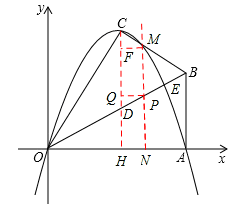
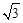 t代入
t代入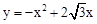 ,得
,得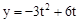 ,
,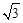 t,﹣
t,﹣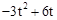 ),F(
),F(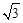 ,
,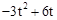 )。
)。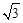 ,t),D(
,t),D(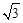 ,1)。
,1)。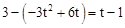 ,解得t=
,解得t=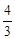 ,t=1(舍去)。
,t=1(舍去)。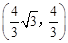 。
。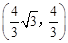


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源:不詳 題型:解答題
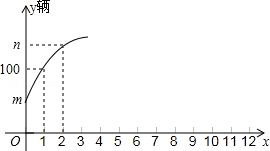
| 時段 | x | 還車數(輛) | 借車數(輛) | 存量y(輛) |
| 6:00﹣7:00 | 1 | 45 | 5 | 100 |
| 7:00﹣8:00 | 2 | 43 | 11 | n |
| … | … | … | … | … |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
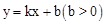 與拋物線
與拋物線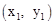 相交于A
相交于A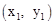 ,B
,B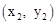 兩點,與x軸正半軸相交于點D,與y軸相交于點C,設△OCD的面積為S,且
兩點,與x軸正半軸相交于點D,與y軸相交于點C,設△OCD的面積為S,且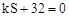 。
。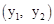 在反比例函數
在反比例函數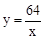 的圖象上;
的圖象上;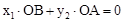 。
。
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 與x軸交于A,B兩點(點A在點B左側),與y軸交于點C,點D為頂點.
與x軸交于A,B兩點(點A在點B左側),與y軸交于點C,點D為頂點.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
| A.y=3x2+2 | B.y=3(x﹣1)2 |
| C.y=3(x﹣1)2+2 | D.y=2x2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com