
 如圖,△ABP中,∠APB=120°,點C、D在線段AB上,△PCD是等邊三角形,請根據所述條件,判斷下列論斷:①CD2=AC•DB;②AP2=AC•AB;③AP•PC=PD•PB;④BP2-BD2=AD•DB,其中正確的個數是
如圖,△ABP中,∠APB=120°,點C、D在線段AB上,△PCD是等邊三角形,請根據所述條件,判斷下列論斷:①CD2=AC•DB;②AP2=AC•AB;③AP•PC=PD•PB;④BP2-BD2=AD•DB,其中正確的個數是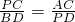 ,
,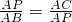 ,
,

 華東師大版一課一練系列答案
華東師大版一課一練系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中數學 來源: 題型:閱讀理解
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,△ABP中,∠APB=120°,點C、D在線段AB上,△PCD是等邊三角形,請根據所述條件,判斷下列論斷:①CD2=AC•DB;②AP2=AC•AB;③AP•PC=PD•PB;④BP2-BD2=AD•DB,其中正確的個數是( )
如圖,△ABP中,∠APB=120°,點C、D在線段AB上,△PCD是等邊三角形,請根據所述條件,判斷下列論斷:①CD2=AC•DB;②AP2=AC•AB;③AP•PC=PD•PB;④BP2-BD2=AD•DB,其中正確的個數是( )查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com