
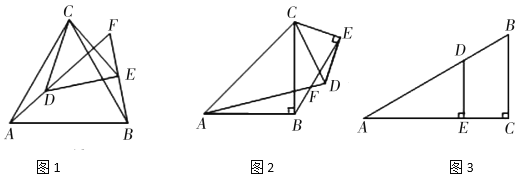
【題目】(1)問題發現
如圖1,![]() 和
和![]() 均為等邊三角形,直線AD和直線BE交于點F.
均為等邊三角形,直線AD和直線BE交于點F.
填空:①![]() 的度數是____;②線段AD,BE之間的數量關系為________;
的度數是____;②線段AD,BE之間的數量關系為________;
(2)類比探究
如圖2,![]() 和
和![]() 均為等腰直角三角形,
均為等腰直角三角形,![]() ,直線AD和直線BE交于點F.請判斷
,直線AD和直線BE交于點F.請判斷![]() 的度數及線段AD,BE之間的數量關系,并說明理由,
的度數及線段AD,BE之間的數量關系,并說明理由,
(3)如圖3,在![]() 中,
中,![]() ,點D在AB邊上,
,點D在AB邊上,![]() ,
,![]() ,將
,將![]() 繞著點A在平面內旋轉,請直接寫出直線DE經過點B時,點C到直線DE的距離.
繞著點A在平面內旋轉,請直接寫出直線DE經過點B時,點C到直線DE的距離.
【答案】(1)①60;②![]() ;(2)∠AFB=45°,AD=
;(2)∠AFB=45°,AD=![]() BE;理由見解析;(3)
BE;理由見解析;(3)![]() ±
±![]()
【解析】
(1)證明△ACD≌△BCE(SAS),即可解決問題;
(2)結論:∠AFB=45°,AD=![]() BE.證明△ACD∽△BCE,可得
BE.證明△ACD∽△BCE,可得![]() ,∠CBF=∠CAF,由此即可解決問題;
,∠CBF=∠CAF,由此即可解決問題;
(3)分兩種情形分別求解即可解決問題.
解:(1)如圖1中,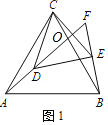
∵△ABC和△CDE均為等邊三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ACD=∠CBF,
設BC交AF于點O.
∵∠AOC=∠BOF,
∴∠BFO=∠ACO=60°,
∴∠AFB=60°,
故答案為60°,AD=BE.
(2)結論:∠AFB=45°,AD=![]() BE.
BE.
理由:如圖2中,
∵∠ABC=∠DEC=90°,AB=BC,DE=EC,
∴∠ACD=45°+∠BCD=∠BCE,![]() ,
,
∴△ACD∽△BCE,
∴![]() ,∠CBF=∠CAF,
,∠CBF=∠CAF,
∴AD=![]() BE
BE
∵∠AFB+∠CBF=∠ACB+∠CAF,
∴∠AFB=∠ACB=45°.
(3)如圖3中,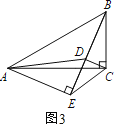
∵AEB=∠ACB=90°,
∴A,B,C,E四點共圓,
∴∠CEB=∠CAB=30°,∠ABD=∠ACE,
∵∠FAE=∠BAC=30°,
∴∠BAD=∠CAE,
∴△BAD∽△CAE,
∴![]() =cos30°=
=cos30°=![]() ,
,
∴EC=![]() BD,
BD,
在Rt△ADE中,∵DE=![]() ,∠DAE=30°,
,∠DAE=30°,
∴AE=![]() DE=3,
DE=3,
∴BE=![]() =4,
=4,
∴BD=BE-DE=4-![]() ,
,
∴CE=![]() BD=2
BD=2![]() -
-![]() ,
,
∵∠BEC=30°,
∴點C到直線DE的距離等于CEsin30°=![]() -
-![]() .
.
如圖4中,當D,EB在同一直線上時,同法可知BD=DE+EB=4+![]() ,CE=
,CE=![]() BD=2
BD=2![]() +
+![]() ,
,
點C到直線DE的距離等于CEsin30°=![]() +
+![]() .
.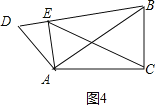
綜上所述,點C到直線DE的距離等于![]() ±
±![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某企業設計了一款工藝品,每件的成本是50元,為了合理定價,投放市場進行試銷.據市場調查,銷售單價是100元時,每天的銷售量是50件,而銷售單價每降低1元,每天就可多售出5件,但要求銷售單價不得低于成本.
![]() 求出每天的銷售利潤
求出每天的銷售利潤![]() 元
元![]() 與銷售單價
與銷售單價![]() 元
元![]() 之間的函數關系式;
之間的函數關系式;
![]() 求出銷售單價為多少元時,每天的銷售利潤最大?最大利潤是多少?
求出銷售單價為多少元時,每天的銷售利潤最大?最大利潤是多少?
![]() 如果該企業要使每天的銷售利潤不低于4000元,且每天的總成本不超過7000元,那么銷售單價應控制在什么范圍內?
如果該企業要使每天的銷售利潤不低于4000元,且每天的總成本不超過7000元,那么銷售單價應控制在什么范圍內?![]() 每天的總成本
每天的總成本![]() 每件的成本
每件的成本![]() 每天的銷售量
每天的銷售量![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近年來網約車十分流行,初三某班學生對“美團”和“滴滴”兩家網約車公司各10名司機月收入進行了一項抽樣調查,司機月收入(單位:千元)如圖所示:

根據以上信息,整理分析數據如下:
平均月收/千元 | 中位數/千元 | 眾數/千元 | 方差/千元 | |
“美團” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
(1)完成表格填空:①__________②__________③__________
(2)若從兩家公司中選擇一家做網約車司機,你會選哪家公司,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
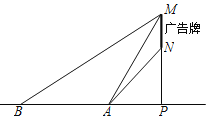
【題目】某數學社團成員想利用所學的知識測量某廣告牌的寬度![]() 圖中線段MN的長
圖中線段MN的長![]() ,直線MN垂直于地面,垂足為點
,直線MN垂直于地面,垂足為點![]() 在地面A處測得點M的仰角為
在地面A處測得點M的仰角為![]() 、點N的仰角為
、點N的仰角為![]() ,在B處測得點M的仰角為
,在B處測得點M的仰角為![]() ,
,![]() 米,且A、B、P三點在一直線上
米,且A、B、P三點在一直線上![]() 請根據以上數據求廣告牌的寬MN的長.
請根據以上數據求廣告牌的寬MN的長.
![]() 參考數據:
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是邊長為
是邊長為![]() 的等邊三角形,邊
的等邊三角形,邊![]() 在射線
在射線![]() 上,且
上,且![]() ,點
,點![]() 從點
從點![]() 出發,沿OM的方向以1cm/s的速度運動,當D不與點A重合時,將
出發,沿OM的方向以1cm/s的速度運動,當D不與點A重合時,將![]() 繞點C逆時針方向旋轉60°得到
繞點C逆時針方向旋轉60°得到![]() ,連接DE.
,連接DE.
(1)如圖1,求證:![]() 是等邊三角形;
是等邊三角形;
(2)如圖2,當6<t<10時,DE是否存在最小值?若存在,求出DE的最小值;若不存在,請說明理由.
(3)當點D在射線OM上運動時,是否存在以D,E,B為頂點的三角形是直角三角形?若存在,求出此時t的值;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知有理數-3,1.
(1)在下列數軸上,標出表示這兩個數的點,并分別用A,B表示;
(2)若|m|=2,在數軸上表示數m的點,介于點A,B之間,在A的右側且到點B距離為5的點表示為n.
①計算m+n-mn;
②解關于x的不等式mx+4<n,并把解集表示在下列數軸上.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的變換點
的變換點![]() 的坐標定義如下:
的坐標定義如下:
當![]() 時,點
時,點![]() 的坐標為
的坐標為![]() ;當
;當![]() 時,點
時,點![]() 的坐標為
的坐標為![]() .
.
(1)點![]() 的變換點
的變換點![]() 的坐標是 ;點
的坐標是 ;點![]() 的變換點為
的變換點為![]() ,連接
,連接![]() ,則
,則![]() °;
°;
(2)已知拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() (點
(點![]() 在點
在點![]() 的左側),頂點為
的左側),頂點為![]() .點
.點![]() 在拋物線
在拋物線上,點
![]() 的變換點為
的變換點為![]() .若點
.若點![]() 恰好在拋物線的對稱軸上,且四邊形
恰好在拋物線的對稱軸上,且四邊形![]() 是菱形,求
是菱形,求![]() 的值;
的值;
(3)若點![]() 是函數
是函數![]() 圖象上的一點,點
圖象上的一點,點![]() 的變換點為
的變換點為![]() ,連接
,連接![]() ,以
,以![]() 為直徑作
為直徑作![]() ,
,![]() 的半徑為
的半徑為![]() ,請直接寫出
,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com