
【題目】如圖1,菱形ABCD中,CH⊥AB,垂足為H,交對角線AC于M,連接BM,且AH=3.
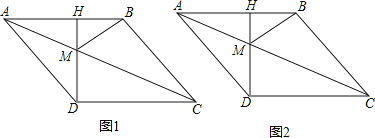
(1)求DM的長;
(2)如圖2,動點P從點A出發,沿折線ABC方向以2個單位/秒的速度向終點C勻速運動,設△PMB的面積為S(S≠0),點P的運動時間為t秒,求S與t之間的函數關系式;
(3)在(2)的條件下,當點P在邊AB上運動時,是否存在這樣的t的值,使∠MPB與∠BCD互為余角?若存在,求出t的值;若不存在,請說明理由.
【答案】(1)DM=![]() (2)S=-
(2)S=-![]() t+
t+![]() 或S=
或S=![]() t-
t-![]() .(3)存在,1.
.(3)存在,1.
【解析】
試題分析:(1)由菱形的性質得到條件,判斷出△AMH∽△CDM,由勾股定理計算出DH,即可;
(2)由△BCM≌△DCM計算出BM=DM,分兩種情況計算即可;
(3)由菱形的性質判斷出△ADM≌△ABM,再判斷出△BMP是等腰三角形,即可.
試題解析:(1)在Rt△ADH中,AD=5,AH=3,
∴DH=4,
∵四邊形ABCD是菱形,
∴AB∥DC,
∴∠BAC=∠DCA,
DH⊥AB,
∴△AMH∽△CDM,
∴![]()
∴![]()
∵DH=4,
∴DM=![]()
(2)在△BCM和△DCM中,
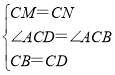
∴△BCM≌△DCM,
∴BM=DM=![]() ,∠CDM=∠CBM=90°
,∠CDM=∠CBM=90°
①當P在AB之間時,S=![]() (5-2t)×
(5-2t)×![]() =-
=-![]() t+
t+![]() .
.
②當P在BC之間時,S=![]() (2t-5)×
(2t-5)×![]() =
=![]() t-
t-![]() .
.
(3)存在,
∵∠ADM+∠BAD=90°,∠BCD=∠BAD,
∴∠ADM+∠BCD=90°,
∵∠MPB+∠BCD=90°,
∴∠MPB=∠ADM,
∵四邊形ABCD是菱形,
∴∠DAM=∠BAM,
∵AM=AM,
∴△ADM≌△ABM,
∴∠ADM=∠ABM,
∴∠MPB=∠ABM,
∵MH⊥AB,
∴PH=BH=![]() ,
,
∴BP=2BH=3,
∵AB=5,
∴AP=2,
∴t=![]() =1.
=1.


科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,將ABCD放置在第一象限,且AB∥x軸.直線y=-x從原點出發沿x軸正方向平移,在平移過程中直線被平行四邊形截得的線段長度l與直線在x軸上平移的距離m的函數圖象如圖2所示,那么AD的長為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,AB的垂直平分線MN交AC于點D,交AB于點E.
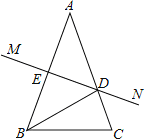
(1)求證:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度數;
(3)若AE=6,△CBD的周長為20,求△ABC的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com