
【題目】已知直線y=![]() x+3與兩坐標軸分別相交于A、B兩點,若點P、Q分別是線段AB、OB上的動點,且點P不與A、B重合,點Q不與O、B重合.
x+3與兩坐標軸分別相交于A、B兩點,若點P、Q分別是線段AB、OB上的動點,且點P不與A、B重合,點Q不與O、B重合.
(1)若OP⊥AB于點P,△OPQ為等腰三角形,這時滿足條件的點Q有幾個?請直接寫出相應的OQ的長;
(2)當點P是AB的中點時,若△OPQ與△ABO相似,這時滿足條件的點Q有幾個?請分別求出相應的OQ的長;
(3)試探究是否存在以點P為直角頂點的Rt△OPQ?若存在,求出相應的OQ的范圍,并求出OQ取最小值時點P的坐標;若不存在,請說明理由.

【答案】(1) 點Q有三個,OQ的長為2或![]() 或
或![]() ;(2) 2個,OQ的長為2或
;(2) 2個,OQ的長為2或![]() ;(3)存在,OQ取最小值時點P的坐標(
;(3)存在,OQ取最小值時點P的坐標(![]() ,
,![]() ).
).
【解析】
試題分析:(1)如圖1中,滿足條件的點Q有三個,分三種情形討論即可①QO=QP,②OP=OQ,③PO=PQ.
(2)如圖2中,滿足條件的點Q有2個.作![]() ⊥OB于
⊥OB于![]() ,
,![]() ⊥OP于
⊥OP于![]() ,可以證明
,可以證明![]() 、
、![]() 滿足條件,理由相似三角形的性質即可解決問題.
滿足條件,理由相似三角形的性質即可解決問題.
(3)存在.以OQ為直徑作⊙G,當⊙G與AB相切于點P時,∠OPQ=90°,此時OQ的值最小.由此求出OQ,即可解決問題.
試題解析:(1)如圖1中,滿足條件的點Q有三個.
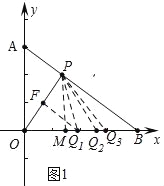
理由:作PM⊥OB于M,作OP的垂直平分線交OP于F,交OB于![]() .則
.則![]() =
=![]() ,△
,△![]() 是等腰三角形,此時
是等腰三角形,此時![]() =
=![]() OB=2.
OB=2.
∵A(0,3),B(4,0),
∴OA=3,OB=4,AB=5,
∵OP⊥AB,
∴![]() OAOB=
OAOB=![]() ABOP,
ABOP,
∴OP=![]() =
=![]() ,
,
當![]() =OP時,△
=OP時,△![]() 是等腰三角形,此時
是等腰三角形,此時![]() =
=![]() ,
,
當PO=![]() 時,∵PM⊥
時,∵PM⊥![]() ,
,
∴![]() =2OM,
=2OM,
∵∠POM=∠![]() ,∠PMO=∠OPB,
,∠PMO=∠OPB,
∴△OPM∽△OBP,
∴![]() =OMOB,
=OMOB,
∴OM=![]() ,
,
∴![]() =
=![]() .
.
綜上所述,△OPQ為等腰三角形時,滿足條件的點Q有三個,OQ的長為2或![]() 或
或![]() .
.
(2)如圖2中,滿足條件的點Q有2個.
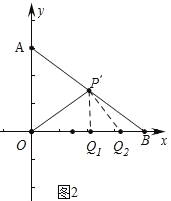
理由:作![]() ⊥OB于
⊥OB于![]() ,
,![]() ⊥OP于
⊥OP于![]() ,
,
∵PA=PB,∠AOB=90°,
∴PA=PB=PO,
∴∠![]() =∠ABO,∵∠
=∠ABO,∵∠![]() =∠AOB,
=∠AOB,
∴△![]() ∽△BAO,
∽△BAO,
∵PA=PB,![]() ∥OA,
∥OA,
∴![]() =
=![]() =
=![]() OB=2,
OB=2,
∵∠![]() =∠ABO,∠
=∠ABO,∠![]() =∠AOB,
=∠AOB,
∴△![]() ∽△BOA,
∽△BOA,
∴![]() ,
,
∴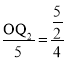 ,
,
∴![]() =
=![]() ,
,
綜上所述,△OPQ與△ABO相似時,滿足條件的點Q有2個,OQ的長為2或![]() .
.
(3)存在.理由如下:
如圖3中,以OQ為直徑作⊙G,當⊙G與AB相切于點P時,∠OPQ=90°,此時OQ的值最小.
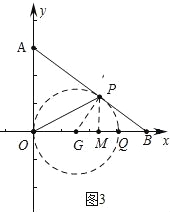
∴設OG=GP=r,
∵AO=AP=3,
∴PB=AB=AP=2,
在Rt△PBG中,∵∠GPB=90°,PG=r,BG=4﹣r,PB=2,
∴![]() ,
,
∴r=![]() ,
,
∴OQ=2r=3,
∴當3≤OQ<4時,△OPQ可為直角三角形.
作PM⊥OB于M.
∵PM∥OA,
∴![]() ,
,
∴![]() ,
,
∴PM=![]() ,BM=
,BM=![]() ,
,
∴OM=4﹣![]() =
=![]() ,
,
∴OQ取最小值時點P的坐標(![]() ,
,![]() ).
).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
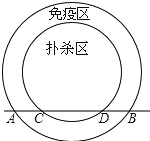
【題目】高致病性禽流感是比SARS傳染速度更快的傳染病.為防止禽流感蔓延,政府規定:離疫點3km范圍內為撲殺區;離疫點3km~5km范圍內為免疫區,對撲殺區與免疫區內的村莊、道路實行全封閉管理.現有一條筆直的公路AB通過禽流感病區,如圖,在撲殺區內公路CD長為4km.
(1)請用直尺和圓規找出疫點O(不寫作法,保留作圖痕跡);
(2)求這條公路在免疫區內有多少千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明做了一個平行四邊形的紙板,但他不確定紙板形狀是否標準,小紅用刻度尺量了這個四邊形的四條邊長,然后告訴小明,紙板是標準的平行四邊形,小紅得出這個結論的依據是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
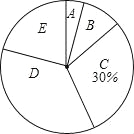
【題目】今年5月份,某校九年級學生參加了南寧市中考體育考試,為了了解該校九年級(1)班同學的中考體育情況,對全班學生的中考體育成績進行了統計,并繪制以下不完整的頻數分布表(如表)和扇形統計圖(如圖),根據圖表中的信息解答下列問題:
(1)求全班學生人數和m的值.
(2)直接寫出該班學生的中考體育成績的中位數落在哪個分數段.
(3)該班中考體育成績滿分共有3人,其中男生2人,女生1人,現需從這3人中隨機選取2人到八年級進行經驗交流,請用“列表法”或“畫樹狀圖法”求出恰好選到一男一女的概率.
分組 | 分數段(分) | 頻數 |
A | 36≤x<41 | 2 |
B | 41≤x<46 | 5 |
C | 46≤x<51 | 15 |
D | 51≤x<56 | m |
E | 56≤x<61 | 10 |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=![]() (k是常數).
(k是常數).
(1)若該函數的圖象與x軸有兩個不同的交點,試求k的取值范圍;
(2)若點(1,k)在某反比例函數圖象上,要使該反比例函數和二次函數y=![]() 都是y隨x的增大而增大,求k應滿足的條件及x的取值范圍;
都是y隨x的增大而增大,求k應滿足的條件及x的取值范圍;
(3)若拋物線y=![]() 與x軸交于A(
與x軸交于A(![]() ,0)、B(
,0)、B(![]() ,0)兩點,且
,0)兩點,且![]() <
<![]() ,
,![]() =34,若與y軸不平行的直線y=ax+b經過點P(1,3),且與拋物線交于
=34,若與y軸不平行的直線y=ax+b經過點P(1,3),且與拋物線交于![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )兩點,試探究
)兩點,試探究![]() 是否為定值,并寫出探究過程.
是否為定值,并寫出探究過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若三角形的三個內角的比是1:2:3,最短邊長為1cm,最長邊長為2cm,則這個三角形三個角度數分別是______,另外一邊的平方是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,對于P(a,b)和點Q(a,b′),給出如下定義:若b′= ,則稱點Q為點P的限變點.例如:點(2,3)的限變點的坐標是(2,3),點(﹣2,5)的限變點的坐標是(﹣2,﹣5).
,則稱點Q為點P的限變點.例如:點(2,3)的限變點的坐標是(2,3),點(﹣2,5)的限變點的坐標是(﹣2,﹣5).
(1)點(![]() ,1)的限變點的坐標是 ;
,1)的限變點的坐標是 ;
(2)判斷點A(﹣2,﹣1)、B(﹣1,2)中,哪一個點是函數y=![]() 圖象上某一個點的限變點?并說明理由;
圖象上某一個點的限變點?并說明理由;
(3)若點P(a,b)在函數y=﹣x+3的圖象上,其限變點Q(a,b′)的縱坐標的取值范圍是﹣6≤b′≤﹣3,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com