
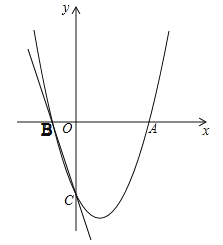
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)經過點A(3,0),B(﹣1,0),C(0,﹣3).
(1)求該拋物線的解析式;
(2)若以點A為圓心的圓與直線BC相切于點M,求切點M的坐標;
(3)若點Q在x軸上,點P在拋物線上,是否存在以點B,C,Q,P為頂點的四邊形是平行四邊形?若存在,求點P的坐標;若不存在,請說明理由.
【答案】(1)y=x2﹣2x﹣3;(2)M(﹣![]() ,﹣
,﹣![]() );(3)存在以點B,C,Q,P為頂點的四邊形是平行四邊形,P的坐標為(1+
);(3)存在以點B,C,Q,P為頂點的四邊形是平行四邊形,P的坐標為(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)或(2,﹣3).
,3)或(2,﹣3).
【解析】
(1)把A,B,C的坐標代入拋物線解析式求出a,b,c的值即可;
(2)由題意得到直線BC與直線AM垂直,求出直線BC解析式,確定出直線AM中k的值,利用待定系數法求出直線AM解析式,聯立求出M坐標即可;
(3)存在以點B,C,Q,P為頂點的四邊形是平行四邊形,分兩種情況,利用平移規律確定出P的坐標即可.
(1)把A(3,0),B(﹣1,0),C(0,﹣3)代入拋物線解析式得: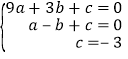 ,
,
解得: ,
,
則該拋物線解析式為y=x2﹣2x﹣3;
(2)設直線BC解析式為y=kx﹣3,
把B(﹣1,0)代入得:﹣k﹣3=0,即k=﹣3,
∴直線BC解析式為y=﹣3x﹣3,
∴直線AM解析式為y=![]() x+m,
x+m,
把A(3,0)代入得:1+m=0,即m=﹣1,
∴直線AM解析式為y=![]() x﹣1,
x﹣1,
聯立得: ,
,
解得: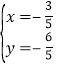 ,
,
則M(﹣![]() ,﹣
,﹣![]() );
);
(3)存在以點B,C,Q,P為頂點的四邊形是平行四邊形,
分兩種情況考慮:
設Q(x,0),P(m,m2﹣2m﹣3),
當四邊形BCQP為平行四邊形時,由B(﹣1,0),C(0,﹣3),
根據平移規律得:﹣1+x=0+m,0+0=﹣3+m2﹣2m﹣3,
解得:m=1±![]() ,x=2±
,x=2±![]() ,
,
當m=1+![]() 時,m2﹣2m﹣3=8+2
時,m2﹣2m﹣3=8+2![]() ﹣2﹣2
﹣2﹣2![]() ﹣3=3,即P(1+
﹣3=3,即P(1+![]() ,3);
,3);
當m=1﹣![]() 時,m2﹣2m﹣3=8﹣2
時,m2﹣2m﹣3=8﹣2![]() ﹣2+2
﹣2+2![]() ﹣3=3,即P(1﹣
﹣3=3,即P(1﹣![]() ,3);
,3);
當四邊形BCPQ為平行四邊形時,由B(﹣1,0),C(0,﹣3),
根據平移規律得:﹣1+m=0+x,0+m2﹣2m﹣3=﹣3+0,
解得:m=0或2,
當m=0時,P(0,﹣3)(舍去);當m=2時,P(2,﹣3),
綜上,存在以點B,C,Q,P為頂點的四邊形是平行四邊形,P的坐標為(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)或(2,﹣3).
,3)或(2,﹣3).


 培優三好生系列答案
培優三好生系列答案 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:初中數學 來源: 題型:
【題目】某商場出售一批進價為2元的賀卡,在營運中發現此商品的日銷價x(單位:元)與銷售量y(單位:張)之間有如下關系:
x/元 | 3 | 4 | 5 | 6 |
y/張 | 20 | 15 | 12 | 10 |
(1)猜測并確定y與x的函數關系式.
(2)當日銷售單價為10元時,賀卡的日銷售量是多少張?
(3)設此卡的利潤為W元,試求出W與x之間的函數關系式,若物價部門規定此卡的銷售單價不能超過10元,試求出當日銷售單價為多少元時,每天獲得的利潤最大并求出最大的利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y= -3x+6的圖象與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點.
兩點.
(1)將直線![]() 向左平移1個單位長度,求平移后直線的函數關系式;
向左平移1個單位長度,求平移后直線的函數關系式;
(2)求出平移過程中,直線![]() 在第一象限掃過的圖形的面積.
在第一象限掃過的圖形的面積.
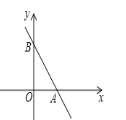
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某青春黨支部在精準扶貧活動中,給結對幫扶的貧困家庭贈送甲、乙兩種樹苗讓其栽種.已知乙種樹苗的價格比甲種樹苗貴10元,用480元購買乙種樹苗的棵數恰好與用360元購買甲種樹苗的棵數相同.
(1)求甲、乙兩種樹苗每棵的價格各是多少元?
(2)在實際幫扶中,他們決定再次購買甲、乙兩種樹苗共50棵,此時,甲種樹苗的售價比第一次購買時降低了10%,乙種樹苗的售價不變,如果再次購買兩種樹苗的總費用不超過1500元,那么他們最多可購買多少棵乙種樹苗?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的材料:
∵![]() =
=![]() ×
×![]() ,
,![]() =
=![]() ×
×![]() ,
,![]() =
=![]() ×
×![]() ,…,
,…,![]() =
=![]() ×
×![]() ,
,
∴![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() ×
×![]() +
+![]() ×
×![]() +
+![]() ×
×![]() +…+
+…+![]() ×
×![]()
=![]() ×
×![]() =
=![]() ×
×![]() =
=![]() .
.
請解答下列問題:
(1)在和式![]() +
+![]() +
+![]() +…中,第100項是 ;
+…中,第100項是 ;
(2)化簡![]() +
+![]() +
+![]() +…+
+…+![]() ,并求n=100時分式的值;
,并求n=100時分式的值;
(3)根據上面的方法,解方程:![]() +
+![]() +
+![]() =
=![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
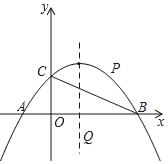
【題目】如圖,已知點A(﹣1,0),B(3,0),C(0,1)在拋物線y=ax2+bx+c上.
(1)求拋物線解析式;
(2)在直線BC上方的拋物線上求一點P,使△PBC面積為1;
(3)在x軸下方且在拋物線對稱軸上,是否存在一點Q,使∠BQC=∠BAC?若存在,求出Q點坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】乘法公式的探究及應用.
數學活動課上,老師準備了若干個如圖![]() 的三種紙片,
的三種紙片,![]() 種紙片邊長為
種紙片邊長為![]() 的正方形,
的正方形,![]() 種紙片是邊長為
種紙片是邊長為![]() 的正方形,
的正方形,![]() 種紙片長為
種紙片長為![]() 、寬為
、寬為![]() 的長方形,并用
的長方形,并用![]() 種紙片一張,
種紙片一張,![]() 種紙片一張,
種紙片一張,![]() 種紙片兩張拼成如圖
種紙片兩張拼成如圖![]() 的大正方形.
的大正方形.

(1)請用兩種不同的方法求圖![]() 大正方形的面積.
大正方形的面積.
方法1:__________________________;
方法2:__________________________.
(2)觀察圖![]() ,請你寫出下列三個代數式:
,請你寫出下列三個代數式:![]() ,
,![]() ,
,![]() 之間的等量關系_____________________.
之間的等量關系_____________________.
(3)根據(2)題中的等量關系,解決如下問題:
①已知:![]() ,
,![]() ,求
,求![]() 的值;
的值;
②已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=![]() x2+bx+c的圖象交x軸于A、D兩點,并經過B點,已知A點坐標是(2,0),B點坐標是(8,6).
x2+bx+c的圖象交x軸于A、D兩點,并經過B點,已知A點坐標是(2,0),B點坐標是(8,6).
(1)求二次函數的解析式;
(2)求函數圖象的頂點坐標及D點的坐標;
(3)二次函數的對稱軸上是否存在一點C,使得△CBD的周長最小?若C點存在,求出C點的坐標;若C點不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
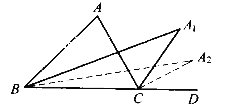
【題目】如圖,在![]() ABC中,
ABC中, ![]() A=80
A=80![]() ,
, ![]() ABC與
ABC與![]() ACD的平分線交于點A1,得
ACD的平分線交于點A1,得![]() A1;
A1; ![]() A1BC與
A1BC與![]() A1CD的平分線相交于點A2,得
A1CD的平分線相交于點A2,得![]() A2;……;
A2;……; ![]() A7BC與
A7BC與![]() A7CD的平分線相交于點A8,得
A7CD的平分線相交于點A8,得![]() A8,則
A8,則![]() A8的度數為()
A8的度數為()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com