
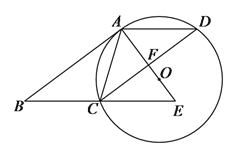
【題目】如圖,在□ABCD中,AC=AD,⊙O是△ACD的外接圓,BC的延長線與AO的延長線交于E.
(1)求證:AB是⊙O的切線;
(2)若AB=8,AD=5,求OE的長.
【答案】(1)證明參見解析;(2)![]() .
.
【解析】試題分析:(1)由已知得出弧AC=弧AD,由垂徑定理得出OA⊥CD,由平行四邊形的性質得出AB∥CD,AD∥BC,AD=BC,因此OA⊥AB,即可得出結論;(2)連接OD,由垂徑定理得出CF=DF=4,由平行線得出△ADF∽△ECF,得出對應邊成比例,證出AD=CE,AF=EF,得出BC=CE,BE=10,由勾股定理求出AE,得出AF=EF=3,設OE=x,則OF=3﹣x,⊙O的半徑為6﹣x,由勾股定理得出方程,解方程即可.
試題解析:(1)∵AC=AD,∴弧AC=弧AD,∴OA⊥CD,∵四邊形ABCD是平行四邊形,∴AB∥CD,AD∥BC,AD=BC,∴OA⊥AB,∴AB是⊙O的切線;(2)連接OD,如圖所示:∵OA⊥CD,∴CF=DF=4,∵AD∥BC,∴△ADF∽△ECF,∴![]() =1,∴AD=CE,AF=EF,∴BC=CE,∴BE=2BC=2AD=10,∴AE=
=1,∴AD=CE,AF=EF,∴BC=CE,∴BE=2BC=2AD=10,∴AE=![]() =6,∴AF=EF=3,設OE=x,則OF=3﹣x,⊙O的半徑為6﹣x,由勾股定理得:OF2+DF2=OD2,即(6﹣x)2=(3﹣x)2+42,解得:x=
=6,∴AF=EF=3,設OE=x,則OF=3﹣x,⊙O的半徑為6﹣x,由勾股定理得:OF2+DF2=OD2,即(6﹣x)2=(3﹣x)2+42,解得:x=![]() ,即OE=
,即OE=![]() .
.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:
【題目】少先隊從夏令營到學校,先下山再走平路,一隊員騎自行車以每小時12千米的速度下山,以每小時9千米的速度走平路,到學校共用了55分鐘,回來時,通過平路的速度不變,但以每小時6千米的速度上山,回到營地共花去了70分鐘的時間,問夏令營到學校多少千米?(列方程計算)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:已知,如圖(1),在面積為S的△ABC中, BC=a,AC=b, AB=c,內切圓O的半徑為r連接OA、OB、OC,△ABC被劃分為三個小三角形.
![]()
∴![]() .
.

(1)類比推理:若面積為S的四邊形ABCD存在內切圓(與各邊都相切的圓),如圖(2),各邊長分別為AB=a,BC=b,CD=c,AD=d,求四邊形的內切圓半徑r;
(2)理解應用:如圖(3),在等腰梯形ABCD中,AB∥DC,AB=21,CD=11,AD=13,⊙O1與⊙O2分別為△ABD與△BCD的內切圓,設它們的半徑分別為r1和r2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題是假命題的是( )
A.數軸上的每一個點必定表示一個實數B.每一個實數都可以在數軸上表示出來
C.數軸上的每一個點必定表示一個有理數D.每一個有理數都可以在數軸上表示出來
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,邊長為2的正方形ABCD,點P在射線BC上,將△ABP沿AP向右翻折,得到△AEP,DE所在直線與AP所在直線交于點F.
(1)如圖1,當點P在邊BC上時:
①若∠BAP=30°,求∠AFD的度數;
②若點P是BC邊上任意一點時(不與B,C重合),∠AFD的度數是否會發生變化?試證明你的結論;
(2)如圖2,若點P在BC邊的延長線上時,∠AFD的度數是否會發生變化?試在圖中畫出圖形,并直接寫出結論;
(3)是否存在這樣的情況,點E為線段DF的中點,如果存在,求BP的值;如果不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若二次函數y=x2﹣6x+9的圖象,經過A(﹣1,y1),B(1,y2),C(4,y3)三點,y1,y2,y3大小關系正確的是( )
A.y1>y2>y3B.y1>y3>y2C.y2>y1>y3D.y3>y1>y2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com