
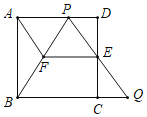
【題目】如圖,在邊長為l的正方形ABCD中,E是邊CD的中點,點P是邊AD上一點(與點A、D不重合),射線PE與BC的延長線交于點Q.
(1)求證:![]() ;
;
(2)過點E作![]() 交PB于點F,連結AF,當
交PB于點F,連結AF,當![]() 時,①求證:四邊形AFEP是平行四邊形;
時,①求證:四邊形AFEP是平行四邊形;
②請判斷四邊形AFEP是否為菱形,并說明理由.
【答案】(1)見解析;(2)①見解析;②當![]() 時,四邊形AFEP是菱形
時,四邊形AFEP是菱形
【解析】
(1)由四邊形ABCD是正方形知![]() ,由E是CD的中點知
,由E是CD的中點知![]() ,結合
,結合![]() 即可得證;
即可得證;
(2)①由![]() 知
知![]() ,結合
,結合![]() 得
得![]() ,由
,由![]() 知
知![]() ,再由
,再由![]() 知
知![]() ,根據
,根據![]() 中
中![]() 知
知![]() ,從而得
,從而得![]() ,據此即可證得
,據此即可證得![]() ,從而得證;
,從而得證;
②設![]() ,則
,則![]() ,若四邊形AFEP是菱形,則
,若四邊形AFEP是菱形,則![]() ,由
,由![]() 得關于x的方程,解之求得x的值,從而得出四邊形AFEP為菱形的情況.
得關于x的方程,解之求得x的值,從而得出四邊形AFEP為菱形的情況.
解:(1)![]() 四邊形ABCD是正方形,
四邊形ABCD是正方形,
![]() ,
,
![]() E是CD的中點,
E是CD的中點,
![]() ,
,
又![]() ,
,
![]() ;
;
(2)①![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四邊形AFEP是平行四邊形;
四邊形AFEP是平行四邊形;
②當![]() 時,四邊形AFEP是菱形.
時,四邊形AFEP是菱形.
設![]() ,則
,則![]() ,
,
若四邊形AFEP是菱形,則![]() ,
,
![]() ,E是CD中點,
,E是CD中點,
![]() ,
,
在![]() 中,由
中,由![]() 得
得![]() ,
,
解得![]() ,
,
即當![]() 時,四邊形AFEP是菱形.
時,四邊形AFEP是菱形.


科目:初中數學 來源: 題型:
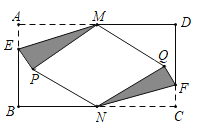
【題目】如圖, 在矩形紙片![]() 中,
中, ![]() , 點
, 點![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點, 點
的中點, 點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上, 且
上, 且![]() .將
.將![]() 沿
沿![]() 折疊, 點
折疊, 點![]() 的對應點為點
的對應點為點![]() ,將
,將![]() 沿
沿![]() 折疊, 點
折疊, 點![]() 的對應點為點
的對應點為點![]() ,當四邊形
,當四邊形![]() 為菱形時, 則
為菱形時, 則![]() _______.
_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
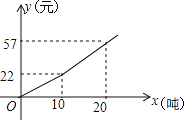
【題目】為鼓勵市民節約用水,某市自來水公司按分段收費標準收費,右圖反映的是每月收水費y(元)與用水量x(噸)之間的函數關系
(1)小紅家五月份用水8噸,應交水費_____元;
(2)按上述分段收費標準,小紅家三、四月份分別交水費36元和19.8元,問四月份比三月份節約用水多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
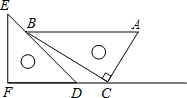
【題目】三角板是我們學習數學的好幫手.將一對直角三角板如圖放置,點C在FD的延長線上,點B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,則CD的長度是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB=DB,∠1=∠2,請問添加下面哪個條件不能判斷△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com